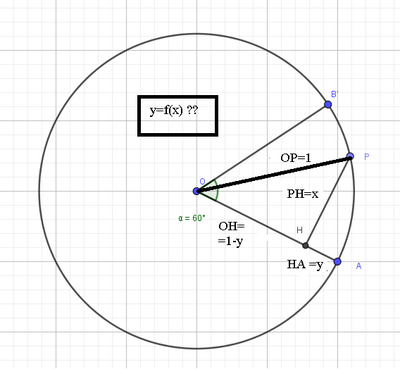
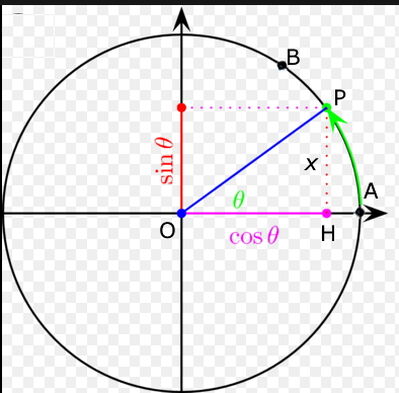
E' dato l'arco AB, sesta parte di una circonferenza di centro O e raggio 1. Indichiamo con P un generico punto di tale arco e sia H la sua proiezione sul raggio OA. Scrivi l'equazione della funzione che esprime la misura y del segmento HA in funzione della misura x del segmento PH.
Quali sono le limitazioni geometriche per la variabile x?
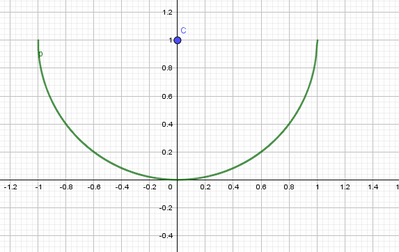
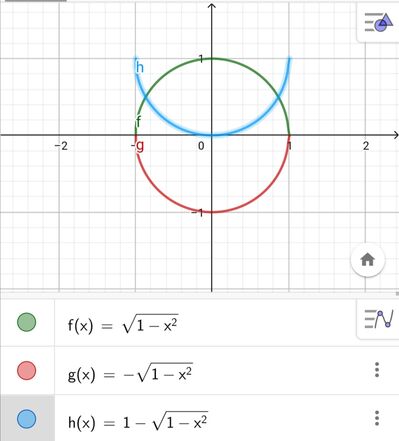
Rappresenta poi graficamente la funzione ottenuta, indipendentemente dalle limitazioni di x.
92
punti
Livello 1
Ciao di nuovo.
Facciamo riferimento al grafico allegato:
Consideriamo il triangolo rettangolo OPH: per esso vale il teorema di Pitagora:
(1 - y)^2 + x^2 = 1 risolviamo tale equazione rispetto ad y:
y = 1 - √(1 - x^2) ∨ y = √(1 - x^2) + 1
escludiamo la seconda funzione in quanto superiore ad 1
Per P---> A abbiamo x---> 0
Per P---->B abbiamo x---> √3/2 che corrisponde all'altezza di un triangolo equilatero di lato pari ad 1
(corrispondenti a valori della funzione SENO per angoli pari a 0 e 60°=1/6 angolo giro)
Quindi la funzione è definita da:
y = 1 - √(1 - x^2) con 0 < x ≤ √3/2
Se togliamo tali limitazioni alla x otteniamo la funzione che esprime una semicirconferenza avente ordinate y inferiori ad 1:
di raggio 1 e di centro C(0,1)
77286
punti
Genius II
Indichiamo con:
THETA = angolo (POA)
Allora il segmento PH risulta:
PH = x = 1* sin(THETA) 0<THETA<360/6 = 60
Quindi 0<x< (radice (3))/2
Utilizziamo il teorema di Pitagora per trovare OH
OH= radice (OP² - PH²) = radice (1 - x²)
Quindi:
y= HA = OA - OH = 1 - radice (1 - x²)
75838
punti
Genius II
La circonferenza goniometrica è quella di raggio uno.
Tradotto in parole povere quel contorto quesito chiede di esprimere il complemento ad uno del coseno (y = 1 - cos(θ)) in funzione del seno (x = sin(θ)) per 0 <= θ <= π/3.
Dal momento che sin^2(θ) + cos^2(θ) = 1 si ha
y = 1 - cos(θ) =
= 1 - √(1 - sin^2(θ)) =
= 1 - √(1 - x^2)
con la limitazione
* 0 <= θ <= π/3 ≡
≡ sin(0) <= sin(θ) <= sin(π/3) ≡
≡ 0 <= x <= √3/2
---------------
La rappresentazione grafica della funzione
* y = 1 - √(1 - x^2)
senza tener conto della limitazione
* 0 <= x^2 <= 3/4 ≡ 0 <= y <= 1/2
consente di tracciare l'intera semicirconferenza inferiore fino all'ordinata uno anziché solo fino a un mezzo.
---------------
La circonferenza da cui "ritagliare" i due archi (con e senza la limitazione) è quella che si ricava da
* y = 1 - √(1 - x^2) ≡
≡ (y - 1)^2 = 1 - x^2 ≡
≡ x^2 + (y - 1)^2 = 1
di raggio uno e centro (0, 1).
http://www.wolframalpha.com/input?i=%5Bx%5E2--%28y-1%29%5E2%3D1%2C%28y-1%2F2%29*%28y-1%29%3D0%5D
51544
punti
Genius I
@exprof 👍
