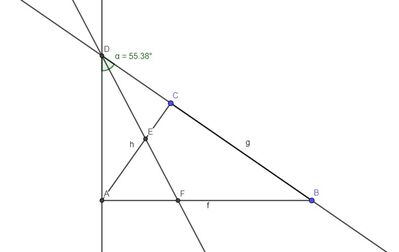
Sia $A B C$ un triangolo rettangolo di ipotenusa $A B$. Traccia la retta passante per il vertice $A$ perpendicolare ad $A B$ e indica con $D$ il suo punto di intersezione con la retta $B C$. Traccia quindi la bisettrice dell'angolo $A \widehat{D} B$ e indica con $E$ (ii) suo punto di intersezione con $A C$ e con $F$ il suo punto di intersezione con $A B$. Dimostra che il triangolo $A F E$ è isoscele sulla base $E F$.
(Suggerimento: indica con $\alpha$ l'ampiezza di $A \widehat{D} B$ ed esprimi in funzione di $\alpha$ le ampiezze degli angoli del triangolo $A F E$ )
Buonasera, potreste aiutarmi a risolvere questo problema di geometria tramite dimostrazione in cui si applica il teorema della somma degli angoli interni di un triangolo.
Grazie mille