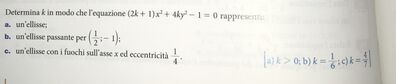Determina $k$ in modo che l'equazione $(2 k+1) x^{2}+4 k y^{2}-1=0$ rappresentce
a. un'ellisse;
b. un'ellisse passante per $\left(\frac{1}{2} ;-1\right)$;
c. un'ellisse con i fuochi sull'asse $x$ ed eccentricità $\frac{1}{4}$.
$\left[\right.$ a) $k>0 ;$ b) $k=\frac{1}{6} ;$ c) $k=\frac{4}{7} \mid$
94
punti
Livello 1
(2·k + 1)·x^2 + 4·k·y^2 - 1 = 0 si deve portare alla forma:
x^2/a^2+y^2/b^2=1
Quindi:
{a^2 = 1/(2·k + 1)
{b^2 = 1/(4·k)
deve essere:
{2·k + 1 > 0
{4·k > 0
quindi: [k > 0]
------------------------------------
Si impone il passaggio per il punto dato:
(2·k + 1)·(1/2)^2 + 4·k·(-1)^2 - 1 = 0
(2·k + 1)/4 + 4·k - 1 = 0
(18·k - 3)/4 = 0-------> k = 1/6 accettabile
--------------------------------------
Affinché i fuochi siano sull'asse delle x deve risultare: a^2>b^2
1/(2·k + 1) > 1/(4·k)
- 1/2 < k < 0 ∨ k > 1/2
Quindi la soluzione è in grassetto!
Poi:
c^2 = a^2 - b^2------> c^2 = 1/(2·k + 1) - 1/(4·k)
c^2 = (2·k - 1)/(4·k·(2·k + 1))
Quindi
e^2 = c^2/a^2------> e^2 = (2·k - 1)/(4·k·(2·k + 1))·(2·k + 1)
e^2 = (2·k - 1)/(4·k)
Quindi:
(2·k - 1)/(4·k) = (1/4)^2-----> (2·k - 1)/(4·k) = 1/16
16·(2·k - 1) = 4·k
32·k - 16 = 4·k------> 28·k = 16----> k = 4/7
77800
punti
Genius II
Ho la vaga impressione d'avere risposto di recente a questa domanda già una volta.
Boh, misteri delle domande reiterate!
---------------
L'equazione
* Γ(k) ≡ (2*k + 1)*x^2 + 4*k*y^2 - 1 = 0 ≡
≡ x^2/(1/(2*k + 1)) + y^2/(1/(4*k)) = 1
rappresenta coniche a centro
* centrate nell'origine
* con assi di simmetria giacenti su quelli coordinati
* con semiassi
** a = 1/√(|2*k + 1|) > 0 (≡ k != - 1/2)
** b = 1/√(|4*k|) > 0 (≡ k != 0)
==============================
RISPOSTE
---------------
a) Γ(k) è un'ellisse se e solo se
* (2*k + 1 > 0) & (4*k > 0) & (k != - 1/2) & (k != 0) ≡ k > 0
---------------
b) Γ(k) è un'ellisse per (1/2, - 1) se e solo se
* ((1/2)^2/(1/(2*k + 1)) + (- 1)^2/(1/(4*k)) = 1) & (k > 0) ≡ k = 1/6
---------------
c1) Γ(k) è un'ellisse coi fuochi sull'asse x se e solo se
* (a > b) & (k > 0) ≡
≡ (1/√(|2*k + 1|) > 1/√(|4*k|)) & (k > 0) ≡ k > 1/2
di semidistanza focale
* c = √(a^2 - b^2) = √(1/(2*k + 1) - 1/(4*k)) =
= √((2*k - 1)/(4*k*(2*k + 1)))
---------------
c2) Γ(k) è un'ellisse coi fuochi sull'asse x ed eccentricità e = 1/4 se e solo se
* (e = c/a = 1/4) & (k > 1/2) ≡
≡ (√((2*k - 1)/(4*k*(2*k + 1)))/(1/√(|2*k + 1|)) = 1/4) & (k > 1/2) ≡
≡ k = 4/7
51854
punti
Genius I
