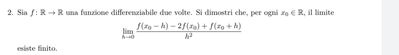Sia $f: \mathbb{R} \rightarrow \mathbb{R}$ una funzione differenziabile due volte. Si dimostri che, per ogni $x_{0} \in \mathbb{R}$, il limite
$$
\lim _{h \rightarrow 0} \frac{f\left(x_{0}-h\right)-2 f\left(x_{0}\right)+f\left(x_{0}+h\right)}{h^{2}}
$$
esiste finito.
39
punti
Livello 0
sappiamo che df/dx = f' = lim(h--->0) (-f(xo) + f(xo+h))/h e d²f/dx² = df'/dx = f'' = lim(h--->0) (-f'(xo) + f'(xo+h))/h = lim(h--->0) (-df(xo)/dx +df(xo+h)/dx)/h
è:
lim(h--->0) (f(xo-h) - 2*f(xo) + f(xo+h))/h² = lim(h--->0) (f(xo-h) - f(xo) -f(xo)+ f(xo+h))/h² = ---> posto to =xo-h ---> = lim(h--->0)[ (f(to) - f(to+h))/h² + f'(xo)/h ]= lim(h--->0) (-f'(to) +f'(to+h))/h = f''(to) che esiste per ipotesi per ogni to
5664
punti
Livello 5
