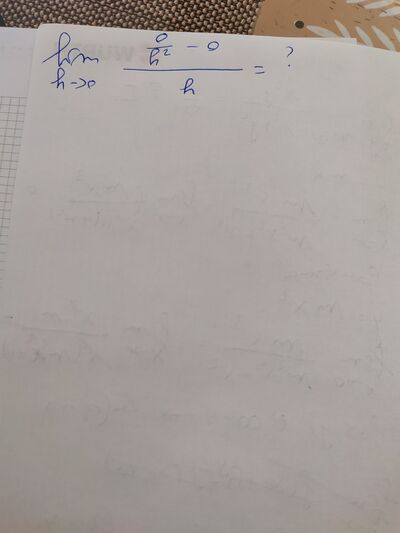[Risolto] Continuità, differenziabilità e piano tangente ad una superficie in un punto dato.

Vediamo se la funzione è continua verificando se:

$lim_{(x,y)\rightarrow (0,0)} f(x,y) = 0$

Calcoliamo quindi:

$ lim_{(x,y)\rightarrow (0,0)} \frac{x^2y}{x^2+y^2} =\frac{[0]}{[0]}$

Sostituiamo $y=mx$:

$lim_{(x,y)\rightarrow (0,0)} \frac{x^2(mx)}{x^2+m^2x^2} =$
$lim_{(x,y)\rightarrow (0,0)} \frac{x^2(mx)}{x^2(1+m^2)}=$
$lim_{(x,y)\rightarrow (0,0)} \frac{mx}{1+m^2} = 0 \forall m \in R$

Poiché il valore del limite è indipendente da $m$, il limite è 0 e la funzione è continua.

---

Passiamo alla verifica della differenziabilità. Calcoliamo le derivate parziali in (0,0) attraverso il limite del rapporto incrementale:

$f_x(0,0) = lim_{h\rightarrow 0}\frac{f(0+h,0)-f(0)}{h} = lim_{h\rightarrow 0}\frac{f(h,0)}{h}$

$lim_{h\rightarrow 0} \frac{\frac{h^2\cdot 0}{h^2+0}}{h} = 0$

Questo limite è semplicemente zero perché abbiamo uno zero che annulla la frazione, quindi prima ancora di sostituire $h\rightarrow 0$, la frazione è già nulla.

Analogamente:

$f_y(0,0) = lim_{h\rightarrow 0}\frac{f(0,0+h)-f(0)}{h} = lim_{h\rightarrow 0}\frac{f(0,h)}{h}$

$lim_{h\rightarrow 0} \frac{\frac{0\cdot h}{0+h^2}}{h}=0$

Una volta calcolate le derivate parziali, calcoliamo il seguente limite, che deve dare come risultato 0:

$ lim_{(h,k)\rightarrow (0,0)} \frac{f(h,k)-f(0,0)-f_x(0,0)h-f_y(0,0)k}{\sqrt{h^2+k^2}}=$ $lim_{(h,k)\rightarrow (0,0)} \frac{f(h,k)}{\sqrt{h^2+k^2}}$

Otteniamo dunque:

$lim_{(h,k)\rightarrow (0,0)} \frac{\frac{h^2k}{h^2+k^2}}{\sqrt{h^2+k^2}}=$

Al solito sostituiamo $k=mh$ che sarebbe il nostro $y=mx$:

$lim_{(h,k)\rightarrow (0,0)} \frac{\frac{h^2(mh)}{h^2+m^2h^2}}{\sqrt{h^2+m^2h^2}}=$

$lim_{(h,k)\rightarrow (0,0)} \frac{h^2(mh)}{(h^2+m^2h^2)\sqrt{h^2+m^2h^2}}=$

mettendo in evidenza:

$lim_{(h,k)\rightarrow (0,0)} \frac{h^3m}{h^2(1+m^2)*h\sqrt{1+m^2}}=$

$lim_{(h,k)\rightarrow (0,0)} \frac{m}{(1+m^2)*\sqrt{1+m^2}}$

il limite dipende da m e dunque non esiste. Questo ci dice che quindi la funzione non è differenziabile in (0,0).

---

Infine calcoliamo il piano tangente in $(1,2,f(1,2))$ mediante l'equazione:

$ z = f(1,2) +f_x(1,2)(x-1) + f_y(1,2)(y-2)$

Nota che in $(x,y)=(1,2)$ la funzione è differenziabile, a differenza di (0,0).

Calcoliamo i termini che ci servono:

$ f(1,2) = \frac{1*4}{1+4} = \frac{4}{5}$

Calcoliamo le derivate parziali attraverso le classiche regole di derivazione (non serve il rapporto incrementale: la funzione è continua nel punto):

$ f_x(x,y)= \frac{2xy(x^2+y^2)-x^2y(2x)}{(x^2+y^2)^2}$

$f_x(1,2) = \frac{4(1+4)-4}{(1+4)^2} = \frac{16}{25}$

e rispetto a y:

$f_y(x,y) = \frac{x^2(x^2+y^2)-x^2y(2y)}{(x^2+y^2)^2}$

$f_y(1,2) = \frac{(1+4)-8}{(1+4)^2} = \frac{-3}{25}$

Dunque abbiamo:

$ z = \frac{4}{5} + \frac{16}{25}(x-1) -\frac{3}{25}(y-2)$

volendo risistemarla un poco otteniamo:

$ 16x -3y-25z+10=0$

 

Noemi