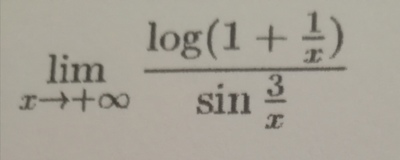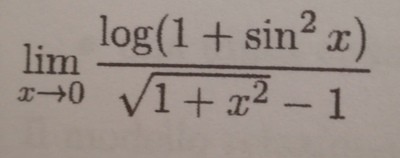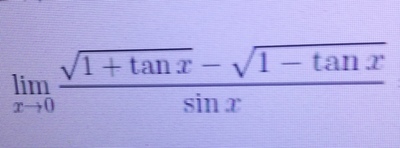Ciao!Sono sempre alle prese con la risoluzione di limiti senza l'uso di De L'Hopital o serie di Taylor.Purtroppo non so come andare avanti.Si accettano consigli sulla strategia di risoluzione dei limiti.Mi riferisco in generale e non solo ai limiti in foto.Grazie ancora!:)
Ho pensato di ricondurre il numeratore di questo limite per x-> +infinito al limite notevole di log(1+x)^x .Il problema è che non ho la x da elevare ad (1+x) e quindi per ricavarmela,ho pensato di racconglierla log x(1/x+1) e poi ho pensato di intendere la x di raccoglimento come il suo reciproco ovvero 1/x in modo tale da elevarlo ad (1/x +1) per ottenere in pratica (1/x +1)^1/x = e. Ho poi pensato di effettuare un cambio di variabile ponendo y=1/x. A quel punto ho ottenuto (1+y)^y ma non so se questa cosa si possa fare.Al denominatore sin 3/x, ho aggiunto un 3 alla x e poi ho moltiplicato per 3x perchè la mia idea era moltiplicare e dividere per la stessa quantità ma mi sembra tutto molto forzato.
Qui non sapevo proprio cosa fare.L'unica cosa che mi è venuta in mente è intendere sen^2x come (1-cos^2x).
Qui,a parte considerare tanx come sinx/cosx,non mi è venuto in mente niente.Forse bisognava raccogliere sinx sia al numeratore che al denominatore.Il mio scopo era tentare di ricondurre sia il numeratore che il denominatore a possibili limiti notevoli ma non mi è riuscito niente.