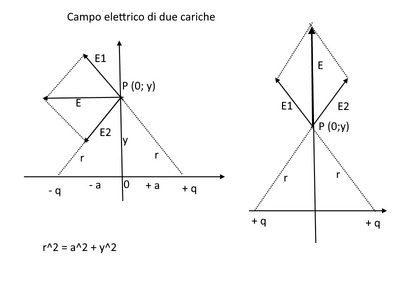
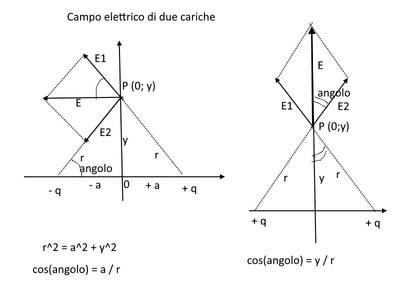
Ognuna delle due cariche genera un campo elettrico di intensità $\dfrac{1}{4\pi \epsilon_{0}} \cdot \dfrac{q}{r^{2}}$ in cui $r^{2} \,=\, a^{2} + y^{2}$ (teorema di Pitagora).
Posso suddividere il campo elettrico con le due componenti lungo l'asse $x$ e lungo l'asse $y$.
Per la carica $-q$ :
$E_{x1} \,=\, \dfrac{1}{4\pi \epsilon_{0}} \cdot \dfrac{q}{a^{2} + y^{2}} \cdot cos(\theta) \,(-u_{x})$
$E_{y1} \,=\, \dfrac{1}{4\pi \epsilon_{0}} \cdot \dfrac{q}{a^{2} + y^{2}} \cdot sen(\theta) \,(-u_{y})$
Per la carica $q$ :
$E_{x2} \,=\, \dfrac{1}{4\pi \epsilon_{0}} \cdot \dfrac{q}{a^{2} + y^{2}} \cdot cos(\theta) \,(-u_{x})$
$E_{y2} \,=\, \dfrac{1}{4\pi \epsilon_{0}} \cdot \dfrac{q}{a^{2} + y^{2}} \cdot sen(\theta) \,(u_{y})$
($\theta$ è l'angolo formato tra l'asse $x$ e il segmento che congiunge una delle cariche col punto $(0,y)$, uguale per entrambe le cariche).
Lungo l'asse $y$ le componenti generate hanno stessa intensità e verso opposto e quindi si annullano.
Le componenti lungo l'asse $x$ invece , oltre ad avere la stessa intensità, sono di verso concorde $(-u_{x})$.
$E \,=\, \dfrac{1}{4\pi \epsilon_{0}} \cdot \dfrac{2q}{a^{2} + y^{2}} \cdot cos(\theta) \,(-u_{x}) $
Posso riscrivere $cos(\theta)$, infatti dalla trigonometria so che $(a^{2} + y^{2}) \cdot cos(\theta) \,=\, a$
quindi $cos(\theta) \,=\, \dfrac{a}{a^{2} + y^{2}}$
$E \,=\, \dfrac{1}{4\pi \epsilon_{0}} \cdot \dfrac{2q\cdot a}{(a^{2} + y^{2})^{\frac{3}{2}}}\,(-u_{x}) $
Con lo stesso ragionamento è facile vedere che se la carica in $(-a,0)$ è positiva la componente del campo elettrico lungo l'asse $x$ si annulla mentre lungo l'asse $y$ si somma.
$sen(\theta) \,=\, \dfrac{y}{a^{2} + y^{2}}$
$E \,=\, \dfrac{1}{4\pi \epsilon_{0}} \cdot \dfrac{2q\cdot y}{(a^{2} + y^{2})^{\frac{3}{2}}}\,(u_{y})$