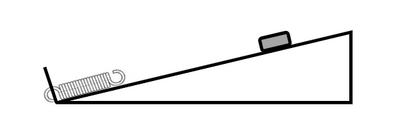
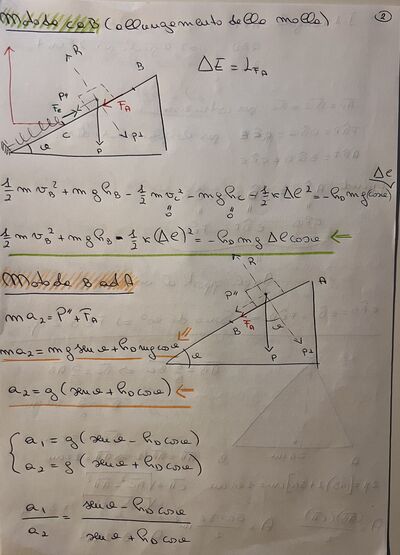
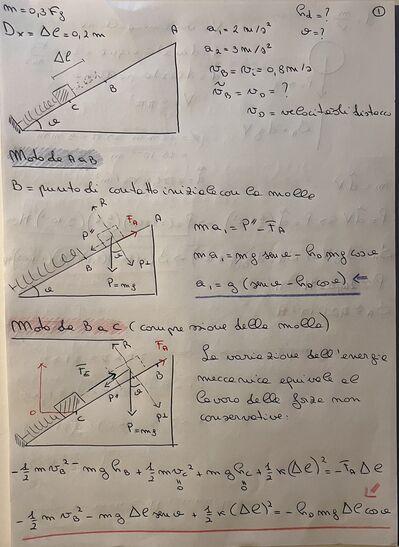
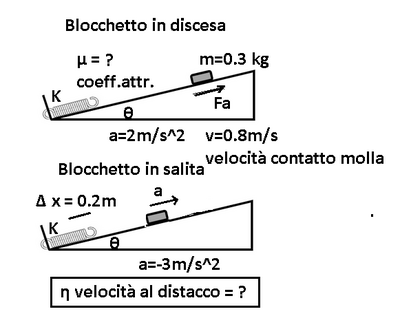
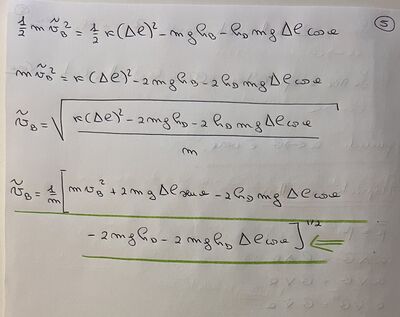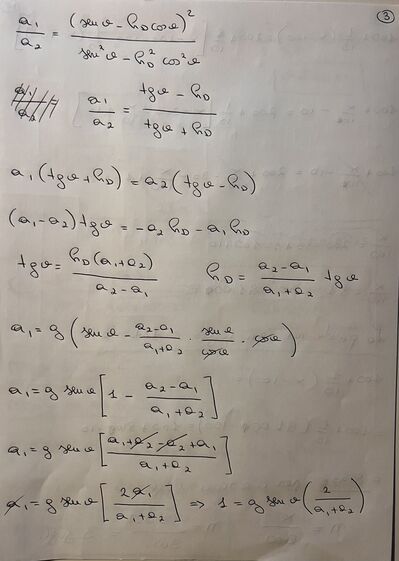Un blocchetto di massa m=0.3Kg, scende lungo un piano inclinato scabro, con inclinazione theta rispetto alla direzione orizzontale e coefficiente di attrito dinamico hd. Al termine del piano è collocata una molla che lo respinge verso l’alto, invertendone il moto. Prima del contatto con la molla, nel moto di discesa si osserva l’accelerazione a1=2m/s2, mentre nel moto di salita, dopo il distacco dalla molla, si osserva l’accelerazione a2=3m/s2, anch’essa diretta verso il basso. Determinare l’angolo di inclinazione ed il coefficiente di attrito dinamico. Sapendo, inoltre, che la massima compressione subita dalla molla è Dx=0.2m e che la velocità del blocchetto nell’istante in cui entra in contatto con la molla è vi= 0.8m/s, determinare la velocità v dal momento del distacco dalla molla.