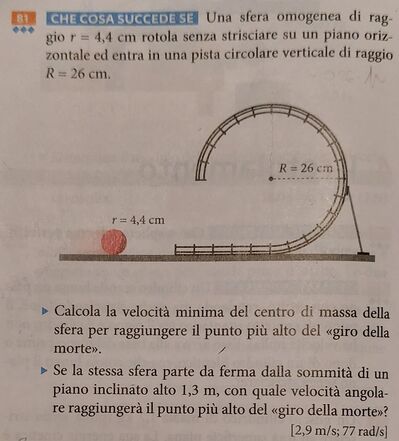
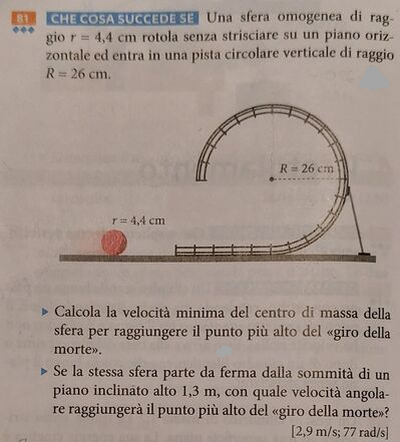
Una sfera omogenea di raggio r=4,4 cm rotola senza strisciare su un piano oriz- zontale ed entra in una pista circolare verticale di raggio R=26 cm.
► Calcola la velocità minima del centro di massa della sfera per raggiungere il punto più alto del <<giro della morte».
Se la stessa sfera parte da ferma dalla sommità di un piano inclinato alto 1,3 m, con quale velocità angola- re raggiungerà il punto più alto del «giro della morte»?
Soluzioni : 2,9 m/s ; 77 rad/s
Grazie mille a chiunque mi aiuterà