Non è la soluzione completa del problema. Più che altro considera questo messaggio come una guida che ti aiuterà a scriverla.
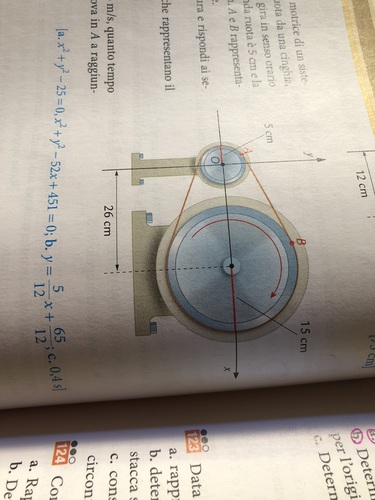
a). Ci sono due circonferenze:
- una di centro nell'origine $C_1(0,0)$ e raggio $r=5$, di equazione
$\gamma_1:(x-x_{C_1})^2+(y-y_{C_1})^2=r^2 \implies x^2+y^2=25$
- una di centro nel punto $C_2(26,0)$ e raggio $R=15$, di equazione
$\gamma_2:(x-x_{C_2})^2+(y-y_{C_2})^2=R^2\implies (x-26)^2+y^2=225$
b) La retta $s$ passante per $A$ e per $B$ è tangente a entrambe le circonferenze. Ciò significa che:
- la distanza tra la retta e il centro della circonferenza $\gamma_1$ deve coincidere col raggio $r=5$;
- la distanza tra la retta e il centro della circonferenza $\gamma_2$ deve coincidere col raggio $R=15$.
Scrivi l'equazione della retta $s$ in forma esplicita
$s: y=mx+q \implies mx-y+q=0$
osserva che $m>0$ perché la retta è crescente, così come è positiva l'ordinata all'origine, e usa la formula della distanza di un punto da una retta.
Affinché $s$ sia tangente a $\gamma_1$, si deve avere che:
$\mbox{distanza}(C_1,s)=r\implies \dfrac{|q|}{\sqrt{m^2+1}}=5$
Affinché $s$ sia tangente a $\gamma_2$, si deve avere invece che:
$\mbox{distanza}(C_2,s)=R\implies \dfrac{|26m+q|}{\sqrt{m^2+1}}=15$
Mettendo a sistema le due equazioni e tenendo conto che $m>0,q>0$, otterrai $m=\dfrac{5}{12},q=\dfrac{65}{12}$.
c) Per rispondere all'ultimo quesito, hai bisogno dei punti di tangenza $A$ e $B$.
Per calcolare le coordinate di $A$, basta mettere a sistema l'equazione di $s$ con quella di $\gamma_1$; Le coordinate di $B$ sono invece soluzioni del sistema costituito dalle equazioni di $s$ e $\gamma_2$.
Trovati $A$ e $B$, ne calcoli la distanza, che se non ho sbagliato i calcoli è $\overline{AB}=24\ \mbox{cm}=0.24\ \mbox{m}$: essa rappresenta lo spazio percorso dal punto materiale.
A questo punto osserva che il punto materiale si muove di moto rettilineo (la cinghia è un segmento) uniforme (la velocità della cinghia è costante), per cui spazio, tempo e velocità sono legati dalla relazione:
$\mbox{spazio}=\mbox{velocit}\grave{\mbox{a}}\cdot\mbox{tempo}$
da cui
$\mbox{tempo}=\dfrac{\mbox{spazio}}{\mbox{velocit}\grave{\mbox{a}}}=\dfrac{0.24 \ \mbox{m}}{0.6\ \mbox{m}/\mbox{s}}=0.4\ \mbox{s}$