Le funzioni goniometriche di angoli associati
Consideriamo un angolo $\alpha $. Chiamiamo angoli associati ( o archi associati) ad $\alpha $ i seguenti angoli:
$-\alpha $, $\frac{\pi }{2} -\alpha $, $\frac{\pi }{2} +\alpha$, $\pi -\alpha $, $\pi +\alpha$, $\frac{3\pi }{2} -\alpha$ , $\frac{3\pi }{2} +\alpha$ , $2\pi -\alpha $
Determiniamo seno, coseno, tangente e cotangente degli angoli associati ad $ \alpha $, in funzione di seno, coseno, tangente e cotangente del’angolo $ \alpha $.
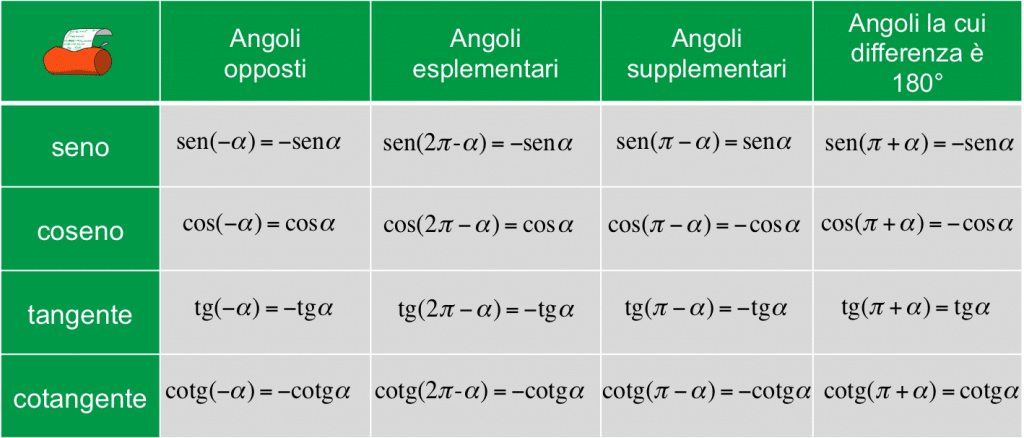
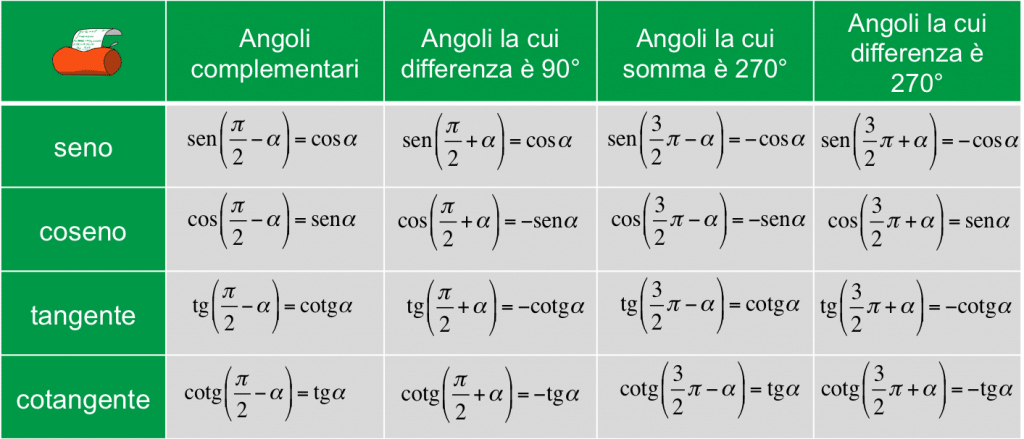
CONSIGLIO PER L’APPRENSIONE MNEMONICA
Quando l’arco associato ha al denominatore 2, la funzione cambia con il suo opposto, ad esempio se è una funzione seno diventerà una funzione coseno. [Tab. 2]
Questa ”regola” non è valida per le funzioni con gli angoli associati interi, ovvero in questo caso permane la natura della funzione. Ad esempio la funzione seno rimarrà seno, quella coseno rimarrà coseno e così via. [Tab. 1]
La riduzione al primo quadrante
Utilizzando le relazioni stabilite per gli angoli associati, è possibile determinare le funzioni goniometriche di qualunque angolo, conoscendo le funzioni goniometriche degli angoli che appartengono al primo quadrante.
Il procedimento relativo viene detto riduzione al primo quadrante.
ESEMPIO
Riduciamo al primo quadrante $\sin 110°$.
Poiché 110°=90°+20° , possiamo scrivere:
$$ \sin 110° = \sin (90° + 20°)=\cos 20°$$
INDICE
- Gli angoli associati
- Le formule goniometriche di addizione e sottrazione
- Le formule goniometriche di duplicazione
- Le formule goniometriche di bisezione
- Le formule goniometriche parametriche
- Le formule di Prostaferesi e di Werner
