La spiegazione di quest'esercizio consiste nel leggerlo trascurando le chiacchiere e mantenendo i significati
A) delle nozioni di cui esso intende verificare che tu abbia conseguito conoscenza e comprensione: unità di misura; sistema Oxy di riferimento ortogonale monometrico levogiro; controllo della propagazione dell'incertezza di misurazione;
B) delle operazioni applicative di dette nozioni di cui esso intende verificare che tu abbia la capacità di individuare ed eseguire: rappresentazione di un vettore come coppia ordinata o di componenti cartesiane o di modulo e anomalia (rispetto al semiasse x > 0); trasformazioni da una rappresentazione all'altra; somma/differenza vettoriale.
---------------
Se alcune delle cose che ho elencato in A e B non t'è perfettamente chiara non proseguire la lettura, ma vai a ripassare: tanto questa risposta, una volta pubblicata, non scappa più, resta lì; quando ritorni la ritrovi immutata.
==============================
Esercizio ORA PROVA TU
---------------
Misure
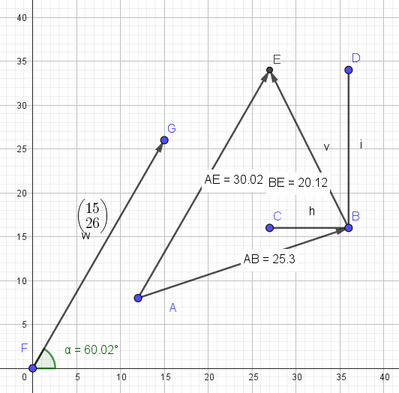
* punti: A(12, 8.0) m, B(36, 16) m
* spostamento: s2(- 9.0, 18) m
* risultati attesi: 45 m, 30 m, 60°
Tutte con due cifre significative: (12, 16, 18, 30, 36, 45) m e 60° esatte; (8.0, - 9.0) m approssimate a ± 5 cm.
---------------
Primo spostamento s1 da A a B (differenza vettoriale fra le posizioni)
* s1 = B - A = (36, 16) - (12, 8.0) = (24, 8.0) m
* √(24^2 + (7.95)^2) <= |s1| <= √(24^2 + (8.05)^2) ≡
≡ √255681/20 <= |s1| <= √256321/20
---------------
Secondo spostamento: s2(- 9.0, 18) m
* √(18^2 + (- 8.95)^2) <= |s2| <= √(18^2 + (- 9.05)^2) ≡
≡ √161641/20 <= |s2| <= √162361/20
---------------
Spostamento totale (somma vettoriale degli spostamenti)
* s = s1 + s2 = (24, 8.0) + (- 9.0, 18) = (15.0, 26.0) m
* √((14.95)^2 + (25.95)^2) <= |s| <= √((15.05)^2 + (26.05)^2) ≡
≡ √358762/20 <= |s| <= √362042/20
------------------------------
RISPOSTE AI QUESITI
---------------
a) Percorso = L = |s1| + |s2| m
* (√255681 + √161641)/20 <= L <= (√256321 + √162361)/20 ~≡
~≡ 45.384755 <= L <= 45.461099
* L = ((45.461099 + 45.384755)/2 ± (45.461099 - 45.384755)/2) =
= (45.422927 ± 0.038172) ~=
~= (45.42 ± 0.04) m
Il risultato atteso (45 m) è discutibile anzitutto perché è scritto come esatto e poi perché ha un valore inferiore al minimo dell'intervallo, frutto di un'approssimazione troppo grossolana.
---------------
b) |s|
* √358762/20 <= |s| <= √362042/20 ~≡
~≡ 29.948372 <= |s| <= 30.084963
* |s| = ((30.084963 + 29.948372)/2 ± (30.084963 - 29.948372)/2) =
= (30.0166675 ± 0.0682955) ~=
~= (30.02 ± 0.07) m
Qui il risultato atteso (30 m) cade nell'intervallo, ma è ancora spacciato come esatto.
---------------
c) Anomalia θ di S(15.0, 26.0) m
Essendo xS > 0, si deve valutare
* θ = arctg(yS/xS)
--------
* 2595/1505 = 519/301 <= yS/xS <= 2605/1495 = 521/299
* arctg(519/301) <= θ <= arctg(521/299)
* θ = ((arctg(521/299) + arctg(519/301))/2 ± (arctg(521/299) - arctg(519/301))/2) ~=
~= (1.0475 ± 0.0023) ~=
~= (60° 1' 6'' ± 7' 49'')
Anche qui il risultato atteso (60°) cade nell'intervallo, ma anche qui è ancora spacciato come esatto.
------------------------------
MIA OPINIONE CONCLUSIVA
L'autore intendeva dare solo misure esatte e il ",0 m" gli è scappato due volte; ma, per carità!, del tutto a sua insaputa.
E poi pretende di verificare negli altri conoscenza, comprensione e capacità applicative.
Che vergogna per la scuola italiana.