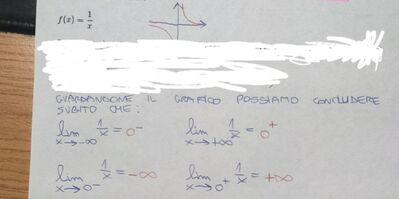
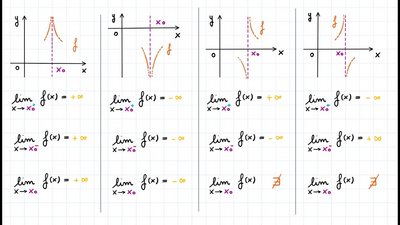
Volevo una spiegazione concettuale/ intuitiva del significato dei limiti tendenti a infinito, ad es. Il limite che tende a -inf. , Io con la x lungo asse ascisse mi sposto verso -inf e fin qua ci sono, in corrispondenza di -inf vedo cosa fa il grafico della funzione, vedo che si avvicina / tende a zero, ora la mia domanda è, il fatto che tenda a 0 (-) è perché io considero come se lo zero fosse lungo le ordinate e quindi se ne considero un suo intorno lungo l asse y(verticale) tocca il valore 0 a six dell'intorno verticale, e per questo fa zero meno??? Cioè il mio dubbio e che non capisco il segno sullo zero da un punto di vista grafico, grazie in anticipo per la rispost