Problemi di Massimo e di minimo di geometria nel piano

Question

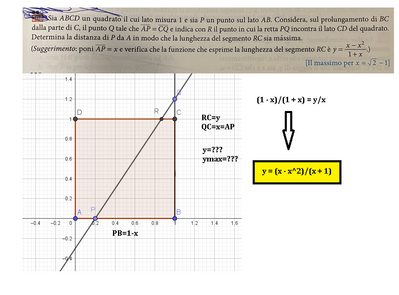
Sia A B C D un quadrato il cui il lato misura 1 e sia P un punto sul lato A B. Considera, sul prolungamento di B C dalla parte di C, il punto Q tale che  overline {A P} a C Q e indica con R il punto in cui la retta P Q incontra il lato C D del quadrato. Determina la distanza di P da A in modo che la lunghezza del segmento R C sia massima.(Suggerimento: poni  overline {A P}=x e verifica che la funzione che esprime la lunghezza del segmento R C e y= frac {x-x^2}{1+x}.)[II massimo per x= sqrt {2}-1$ ] Trovate l’esercizio nella foto è il NUMERO 308 [attach]73314[/attach]

LucianoP · Accepted Answer

[attach]73327[/attach] 0 < x < 1 y' =dy/dx=- (x^2 + 2·x - 1)/(x + 1)^2 impongo la C.N. y'=0 x^2 + 2·x - 1 = 0 risolvo ed ottengo: x = - √2 - 1 ∨ x = √2 - 1 quindi si scarta la prima La derivata seconda: conferma di avere un massimo in quanto  y''  = - 4/(x + 1)^3 < 0 Il valore della funzione è: y max = ((√2 - 1) - (√2 - 1)^2)/((√2 - 1) + 1) y max= 3 - 2·√2

Sebastiano · Answer

Io mi rifiuto di dovere ruotare la figura o di leggere con il collo a 90 gradi. E`compito di chi posta i quesiti essere sicuro che tutto sia fatto per bene (vedi regolamento del sito)

Alfonso3 · Answer

[attach]73326[/attach]

[Risolto] Problemi di Massimo e di minimo di geometria nel piano

Domande