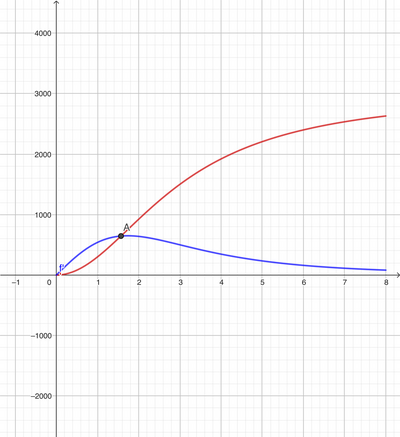
L'andamento delle vendite mensili di un nuovo modello di smartphone segue l'andamento della funzione: f(x)=3000x²/(9+x²), dove x esprime il tempo in mesi e varia in modo continuo nell'intervallo [0;8]
a. Rappresenta graficamente la funzione
b. In quale momento l'aumento delle vendite è massimo?
Guardando il risultato vedo che mi serve il calcolo della derivata seconda ma non ne capisco il motivo