[Risolto] Problema geometrico con equazione

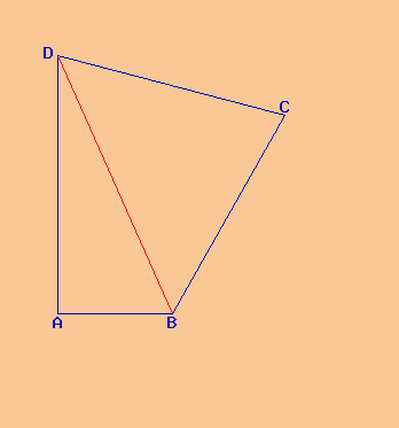
Misure in cm, cm^2.
I triangoli ABD e BDC hanno il lato BD in comune e i vertici A e C nei semipiani opposti rispetto a BD.
Dette (x, y) le loro aree (S(ABD) = x; S(BDC) = y) valgono le seguenti relazioni (equazioni di primo grado)
* (5/8)*x + y/2 = 40
* x + y = 75
che, dovendo valere entrambe, è meglio scrivere insieme (sistema di due equazioni in due incognite).
---------------
* (x + y = 75) & ((5/8)*x + y/2 = 40) ≡
≡ (y = 75 - x) & ((5/8)*x + (75 - x)/2 = 40)
esplicitando y dalla prima e sostituendone l'espressione nella seconda, questa diventa l'equazione risolvente del sistema: una sola equazione di primo grado nell'unica incognita x.
------------------------------
SVOLGIMENTO
---------------
A) Sottrarre membro a membro il secondo membro.
* (5/8)*x + (75 - x)/2 = 40 ≡ (5/8)*x + (75 - x)/2 - 40 = 0
---------------
B) Moltiplicare membro a membro per otto.
* (5/8)*x + (75 - x)/2 - 40 = 0 ≡ 8*(5/8)*x + 8*(75 - x)/2 - 8*40 = 8*0
---------------
C) Sviluppare, commutare, ridurre.
* 8*(5/8)*x + 8*(75 - x)/2 - 8*40 = 8*0 ≡
≡ 5*x + 4*75 - 4*x - 320 = 0 ≡
≡ 5*x - 4*x + 300 - 320 = 0 ≡
≡ x - 20 = 0
---------------
D) Isolare l'incognita.
* x - 20 = 0 ≡ x = 20
---------------
E) Valutare l'incognita sostituita retrosostituendo il valore di x nell'espressione di y
* y = 75 - x = 75 - 20 = 55

dato il quadrilatero ABCD, la diagonale BD lo divide in due triangoli tali che i 5/8 dell'area del triangolo abd addizionata ad 1/2 dell'area del triangolo bdc e' 40 cm^2. Sapendo che l'area del quadrilatero e' 75 cm^2. calcola le aree dei die triangoli. Soluzioni 20cm^2 e 55 cm^2.

Quale e' lo svolgimento con equazioni di primo grado?

5ABD/8+0,5(75-ABD) = 40 

ABD(5/8-1/2) = 40-37,5 

ABD/8 = 2,5

ABD = 20 cm^2

BCD = 75-20 = 55 cm^2