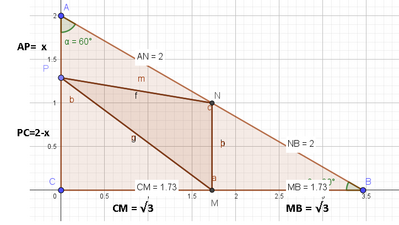
In un triangolo rettangolo $A B C$ l'ipotenusa $A B$ misura 4 e $A \widehat{B C}=30^{\circ}$. Indica con $M$ il punto medio di $B C$ e con $N$ il punto medio di $A B$; preso un punto $P$ sul lato $A C$, tale che $\overline{A P}=x$, determina per quale valore di $x$ è minima la somma dei quadrati delle misure dei lati del triangolo $P M N$.
$$
\left[x=\frac{3}{2}\right.
$$
Non riesco a risolvere questo esercizio. Qualcuno mi aiuta? Grazie
206
punti
Livello 1
ΝΡ^2 = x^2 + 2^2 - 2·(2·x)·COS(60°)
(Th Carnot)
ΝΡ^2 = x^2 - 2·x + 4
ΜΡ^2 = (2 - x)^2 + √3^2
ΜΡ^2 = x^2 - 4·x + 7
ΜΝ^2 = 1^2-----> ΜΝ^2 = 1
Quindi:
y = (x^2 - 2·x + 4) + (x^2 - 4·x + 7) + 1
y = 2·x^2 - 6·x + 12
parabola ad asse verticale minimo in corrispondenza del suo asse
x = - b/(2·a) = 6/4-----> x = 3/2
y min = 2·(3/2)^2 - 6·(3/2) + 12----> ymin = 15/2 = 7.5
77414
punti
Genius II
* f(x) = |MN|^2 +|NP|^2 +|PM|^2
---------------
* AÑM = 120°, perché AɃC = 30° (Ñ e Ƀ col circonflesso in UTF-8 non li trovo)
* CÑM = 60°, perché AɃC = 30°
* |MN| = |AB|/2 = 2, per costruzione.
* |AC| = |AB|/2 = 2, in quanto ABC è metà triangolo equilatero di lato AB.
* |AN| = |NC| = 1, per costruzione.
---------------
* |NP| = ± (x - 1)
I due casi sono
* NP1: P ∈ AN → (|NP| = 1 - x) & (cos(Ñ) = cos(120°) = - 1/2) → |NP|*cos(Ñ) = (x - 1)/2
* NP2: P ∈ NC → (|NP| = x - 1) & (cos(Ñ) = cos(60°) = 1/2) → |NP|*cos(Ñ) = (x - 1)/2
---------------
* |MN|^2 = 4
* |NP|^2 = (x - 1)^2
* |MP|^2 = |MN|^2 + |NP|^2 - 2*|MN|*|NP|*cos(Ñ) =
= 4 + (x - 1)^2 - 2*2*(x - 1)/2 =
= x^2 - 4*x + 7
---------------
* f(x) = |MN|^2 +|NP|^2 +|PM|^2 =
= 4 + (x - 1)^2 +x^2 - 4*x + 7 =
= 2*(x - 3/2)^2 + 15/2
che, a colpo d'occhio, mostra il minimo f(3/2) = 15/2.
51636
punti
Genius I
