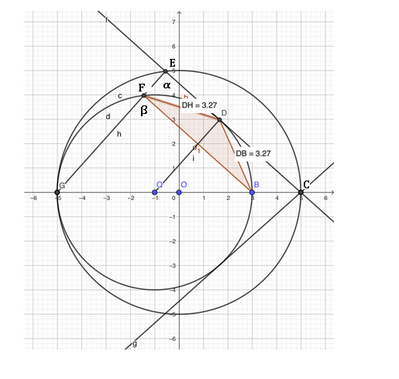
Due circonferenze sono tangenti internamente ad A; inoltre AB è un diametro della circonferenza di raggio minore e AC è un diametro della circonferenza di raggio maggiore. La corda CE della circonferenza di raggio maggiore è tangente in D alla circonferenza di raggio minore e la corda AE interseca la circonferenza di raggio minore in F. Dimostra che il triangolo BDF è isoscele. (Suggerimento: traccia la corda BF)
69
punti
Livello 1
Ciao. Appena posso ti invio risoluzione analitica. Il disegno è utile ma non basta.
Ti ringrazio infinitamente
Fai riferimento al nuovo disegno allegato sopra.
Traccia la corda BF come su suggerimento. Osserva che deve essere : CE//BF in quanto α=β=90° perché tutti e due angoli su semicirconferenze per costruzione. Inoltre il raggio QD di figura della circonferenza minore risulta perpendicolare alla tangente in D e quindi perpendicolare anche a BF che risulta corda della circonferenza interna. Quindi DQ risulta asse della corda (vedi figura) pertanto passante per il punto di mezzo della corda stessa. Quindi relativamente al triangolo BDF, la mediana ed altezza coincidono quindi lo stesso deve essere isoscele.
77312
punti
Genius II
@lucianop grazie mille, quindi per dimostrarlo devo utilizzare solo il disegno? O ci sono anche dei passaggi matematici?
