[Risolto] Potreste aiutarmi con questo problema

89) Prisma:

spigolo laterale $s_{lat}= \frac{180}{3} = 60$ cm;

spigolo di base $s_{b} = \frac{60}{4} = 15$ cm;

perimetro di base $2p_{b} = 3×15 = 45$ cm;

altezza del triangolo equilatero di base $h_{b}= 15×\sqrt{\frac{3}{4}} = 15×0,866 = 12,99$ cm;

area di base $Ab= \frac{15×12,99}{2} = 97,425$ cm²;

area laterale $Al= 2p_{b}×h = 45×60 = 2700$ cm²;

area totale $At= Al+2Ab = 2700+2×97,425 = 2894,85$ cm².

Diciamo L il lato di base e H lo spigolo laterale.

Se 3 H = 180 cm allora H = 4 L = 180 cm/3 = 60 cm => L = 60/4 cm = 15 cm

Area laterale : Pb * H = 3*15 cm * 60 cm = 2700 cm^2

Area di base = rad(3)/4 * 15^2 cm^2 = 97.43 cm^2

Area totale = Area laterale + 2 Area di base = (2700 + 194.86) cm^2 = 2894.86 cm^2

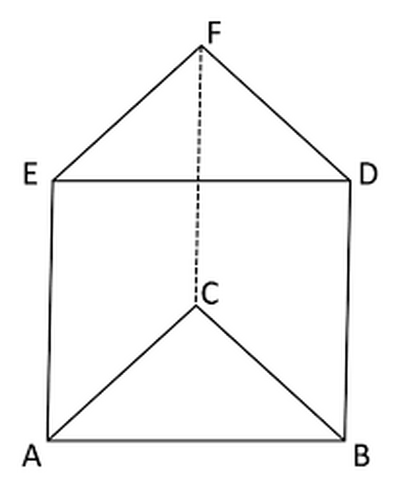
Un prisma retto ha per base un triangolo equilatero. Gli spigoli laterali sono lunghi il quadruplo degli spigoli di base e la loro somma è 180 cm. Calcola l'area laterale Al e totale At.

AE = CF = BD = 180/3 = 60 cm

AB = BC = AC = 60/4 = 15 cm

Al = 15*3*60 = 45*60 = 2.700 cm^2

Ab = 2*(15*0,866*15/2) = 225*0,866 = 194,85 cm^2

At = Al+Ab = 2.700+194,85 = 2.894,85  cm^2