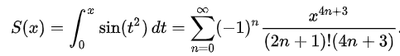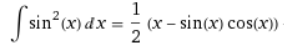Non riesco a risolvere questo due limiti, credo bisogna utilizzare la regola di De l'hopotal ma non riesco, qualcuno riesce?
$$a) \lim _{x \rightarrow 0^{+}} \frac{\int_{0}^{x} \sin t^{2} d t}{\left(e^{x}-1\right)^{6}}$$
$$b) \lim _{x \rightarrow 0^{+}} \frac{\int_{0}^{x^{2}} \sin t^{2} d t}{\left(e^{x}-1\right)^{6}}$$
16
punti
Livello 0
@mymmii ciao scusami ma è $sin^{2}(t)$ o $ sin (t^{2})$?
@mymmii ciao, la domanda fatta sopra è molto pertinente, in quanto se la funzione integranda è $sin(t^2)$ il suo integrale si chiama integrale di Fresnel e ha la seguente espressione:
mentre se la funzione integranda è $sin^2(t)$ la primitiva è molto più abbordabile:
Quindi, quale delle due?
ti faccio il primo, supponendo di utilizzare la regola di de l'Hopital e che la funzione integranda sia $sin^2t$ e non $sin(t^2)$
se derivi rispetto a $x$ il numeratore ritrovi la funzione integranda, quindi una volta derivati sia il numeratore che il denominatore ti ritrovi con:
$\lim_{x \to 0^+} \frac{sin^2x}{6e^x(e^x-1)^5}$
il termine $e^x$ tende a $1$ e il numeratore può essere sostituito con $x^2$:
$\lim_{x \to 0^+} \frac{x^2}{6(e^x-1)^5}$
$\lim_{x \to 0^+} \frac{x^2}{6(e^x-1)^2(e^x-1)^3}$
adesso il termine
$\frac{x^2}{(e^x-1)^2}$ tende ad $1$ e quindi
$\lim_{x \to 0^+} \frac{1}{6(e^x-1)^3}=+\infty$
16169
punti
Livello 9
