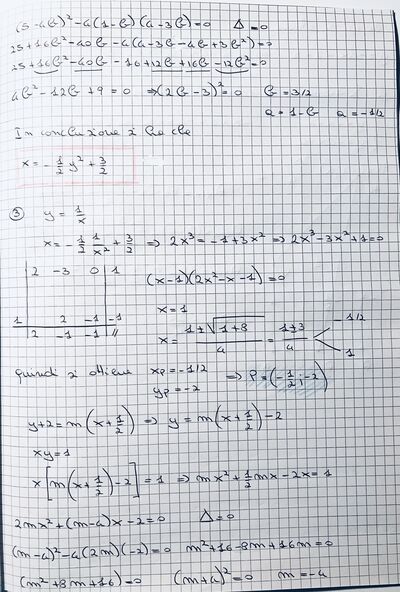Le iperboli equilatere di forma
* Γh(k) ≡ x*y = k^2
avendo il secondo membro non negativo o degenerano sugli assi coordinati per k = 0 oppure hanno centro nell'origine, assi di simmetria le bisettrici dei quadranti, gli assi coordinati per asintoti rami contenuti nei quadranti dispari e vertici V0(- k, - k) e V(k, k).
---------------
1) La retta r, tangente Γh in V, è ortogonale all'asse trasverso y = x
* r(k) ≡ y = 2*k - x
* r(1) ≡ y = 2 - x
---------------
2) La generica parabola di forma
* Γp(a, b) ≡ x = a*y^2 + b
passa per V(k, k) quindi si deve avere
* k = a*k^2 + b ≡ b = k - a*k^2
* Γp(a) ≡ x = a*(y^2 - k^2) + k
Per determinare "a" si fa sistema con la tangente
* r & Γp(a) ≡ (y = 2*k - x) & (x = a*(y^2 - k^2) + k)
e s'impone che s'annulli il discriminante della risolvente
* a*((2*k - x)^2 - k^2) + k - x = 0 ≡
≡ a*x^2 - (4*a*k + 1)*x + 3*a*k^2 + k = 0
* Δ(a) = (2*a*k + 1)^2 = 0 ≡ a = - 1/(2*k)
da cui
* Γp(k) ≡ x = 3*k/2 - y^2/(2*k)
* Γp(1) ≡ x = 3/2 - y^2/2
Vedi al link
http://www.wolframalpha.com/input?i=%5By%3D2-x%2Cx*y%3D1%2Cx%3D3%2F2-y%5E2%2F2%5D
---------------
3a) (x*y = k^2) & (x = 3*k/2 - y^2/(2*k)) ≡
≡ P(- k/2, - 2*k) oppure V(k, k)
Per k = 1, P(- 1/2, - 2) oppure V(1, 1)
---------------
3b) La generica retta per p è y = m*(x + k/2) - 2*k che, a sistema con Γh(k), dà la risolvente
* x*(m*(x + k/2) - 2*k) - k^2 = 0 ≡
≡ 2*m*x^2 + k*(m - 4)*x - 2*k^2 = 0
con discriminante che, per la tangenza, dev'essere zero
* Δ(m) = (k*(m + 4))^2 = 0 ≡ m = - 4
da cui
* t(k) ≡ y = - 4*(x + k)
* t(1) ≡ y = - 4*(x + 1)
Vedi al link
http://www.wolframalpha.com/input?i=%5B%282-x-y%29*%28-4*x-4-y%29%3D0%2Cx*y%3D1%2Cx%3D3%2F2-y%5E2%2F2%5D
---------------
4a) (y = 2*k - x) & (y = - 4*(x + k)) ≡ M(- 2*k, 4*k)
Per k = 1, M(- 2, 4)
---------------
4b) L'area S del triangolo di vertici M(- 2*k, 4*k), P(- k/2, - 2*k), V(k, k) è metà del modulo del prodotto vettoriale fra due qualsiasi lati orientati (vedi in fondo)
* S(MPV) = 27*k^2/4
Per k = 1, S(MPV) = 27/4
==============================
METODO GENERALE per il calcolo dell'area S del triangolo ABC di vertici
* A(a, p), B(b, q), C(c, r)
---------------
Scegliere secondo convenienza uno dei vertici, p.es. C, ed eseguire le sottrazioni di coppie
* CA ≡ A - C = (a, p) - (c, r) = (a - c, p - r)
* CB ≡ B - C = (b, q) - (c, r) = (b - c, q - r)
---------------
Eseguire l'operazione
* CA × CB = (a - c, p - r) × (b - c, q - r) = a*(q - r) + b*(r - p) + c*(p - q)
---------------
Dimezzare il valore assoluto del risultato dà il valore dell'area
* S(ABC) = |CA × CB|/2 = |a*(q - r) + b*(r - p) + c*(p - q)|/2