Ciao!
Mi dite se questa dimostrazione vi pare corretta?
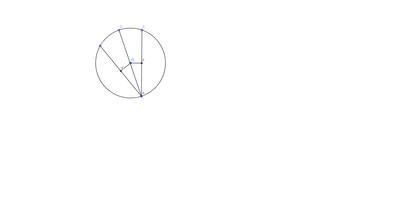
"Siano AB e AC due corde congruenti di una stessa circonferenza. Diomostra che il diametro passante per A è bisettrice dell'angolo alla circonferenza BC"
Chiamo E ed F i punti medi delle corde AB, AC, allora i triangoli AEO, AOF saranno congruenti per terzo criterio, quindi EAO cong FAO e di conseguenza BAD cong. CAD, in quanto AE appartiene ad AB, AF ad AC, AO ad AD.
105
punti
Livello 1
Ho guardato il tuo svolgimento... non mi convince quando ammetti che EO è uguale ad OP (per il terzo criterio tutto e tre i lati dovrebbero essere uguali)...in base a cosa sono uguali? Sinceramente non dico che il tuo svolgimento sia sbagliato ma tale uguaglianza non capisco da dove scaturisce...forse mi sbaglio. Ti allego il mio procedimento...
11946
punti
Livello 7
Grazie per la risposta.
EO=OF perchè AB e AC sono congruenti, quindi, in quanto corde congruenti hanno uguale distanza dal centro.
AE=AF perchè E,F punti medi di corde congruenti
AO è lato in comune.
Quindi AEO ed AFO sono congruenti per terzo criterio.
Stabilito questo, ti pare corretto il resto?
105
punti
Livello 1
@mercurio un'altra cosa... Quando vuoi spiegazioni ad una risposta già data scrivi un commento e non un'altra risposta altrimenti la persona con la quale vuoi parlare non viene taggata e non necessariamente legge quello che scrivi
Grazie del consiglio, ti avevo già scritto un'altra domanda...
Nel tuo svolgimento dici: "a corde congruenti corrispondono archi congreuenti".
Ti riferisci a questo teorema?
https://it.wikipedia.org/wiki/Teorema_sugli_archi_congruenti
Nonostante sembri ovvio ancora non l'avevo incontrato...
105
punti
Livello 1
