[Risolto] Fisica: le molle

Nel testo è detto che a forza peso è trascurabile perché le molle sono in un pian orizzontale.

Le molle, deformate son in configurazione di equilibrio ( 🤔 )

Non vedo l'utilità del dato relativo alla lunghezza a riposo (non serve ai fini de calcolo).

Imponiamo dunque l'equilibrio al sistema delle forze elastiche:

Il testo è semplicemente osceno: in figura non è riportato $L_0$ e non si capisce come la molla 1 venga allungata, se lasciando l'anello in posizione e allungando il punto 1 (in questo caso l'anello si sposterà verso l'alto) oppure se spostando l'anello verso il basso. Le due configurazioni finali sono diverse e quindi le forze delle altre due molle saranno diverse.

la mia risoluzione prevede l'ipotesi che l'anello venga tirato verso il basso. Situazione iniziale con le varie quote (lunghezze):

situazione deformata:

Quindi la molla 2 viene compressa e la molla 3 viene allungata.

Lunghezza molla 2: applichiamo il teorema di Pitagora:

$L_2=\sqrt{(6\sqrt{2})^2+(6\sqrt{2}-4)^2}=\sqrt{72+72+16-48\sqrt{2}}=9.598$ $cm$

Lunghezza molla 3: applichiamo il teorema di Pitagora:

$L_3=\sqrt{12^2+4^2}=\sqrt{160}=12.649$ $cm$

Quindi con le mie ipotesi la molla 2 si accorcia di $2.402$ $cm$ e la molla 3 si allunga di $0.649$ $cm$

I risultati non tornano con quelli del libro, quindi chissà cosa cavolo intendeva il testo...

@debbo_rina @Sebastiano
Il testo è mal scritto, ma fra testo e figura penso ce ne sia abbastanza per fare ipotesi ragionevoli (che gli estremi delle molle siano fissi e l'anello mobile).
Per come la vedo io l'esercizio impegna parecchio in Italiano e in Geometria Analitica e davvero pochissimo in Fisica.
------------------------------
ITALIANO
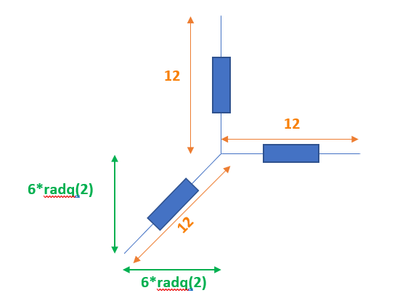
La figura mostra tre molle (1, 2, 3) di egual lunghezza a riposo (12 cm) con un estremo comune fissato a un anello e gli altri tre estremi fissati, in un piano orizzontale, ai punti A, B, C.
L'orizzontalità del piano indica che in questo problema il peso non è in gioco.
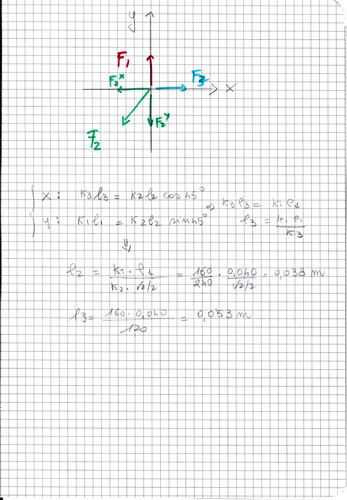
Date le costanti elastiche delle tre molle
* k(1, 2, 3) = (160, 240, 120) N/m
si chiedono gli allungamenti delle molle #2 e #3 nella situazione in cui:
* la molla #1, allungandosi di 4 cm, causa la configurazione di figura in cui:
* l'anello d'ancoraggio si trova nel punto O;
* le molle #1 (OA) e #3 (Oc) si trovano a 90° fra loro;
* la molla #2 (OB) si trova a 135° da ciascuna delle altre due.
------------------------------
GEOMETRIA
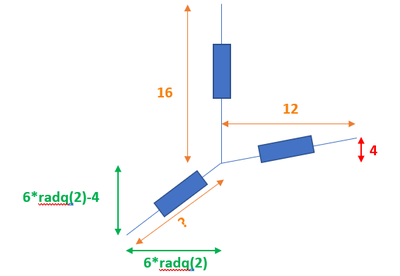
Nel riferimento centimetrico Oxy definito, con (b, c) valori positivi, da
* O(0, 0), A(0, 16), B(- b, - b), C(c, 0)
il punto K(0, 4), posizione dell'anello con tutte le molle a riposo, è centro di una circonferenza Γ di raggio 12
* Γ ≡ x^2 + (y - 4)^2 = 12^2
---------------
Il punto B, sulla retta y = x, si determina dall'intersezione
* (y = x) & (x^2 + (y - 4)^2 = 12^2) ≡
≡ B(2*(1 - √17), 2*(1 - √17)) ~= (- 25/4, - 25/4)
La lunghezza della molla #2 deformata è
* |OB| = √(2*(2*(1 - √17))^2) = 4*√(9 - √17) ~= 8.83347666 ~= 53/6
---------------
Il punto C, sulla retta y = 0, si determina dall'intersezione
* (y = 0) & (x^2 + (y - 4)^2 = 12^2) ≡ C(8*√2, 0) ~= (181/16, 0)
La lunghezza della molla #3 deformata è
* |OC| = 8*√2 ~= 11.313708 ~= 181/16
------------------------------
FISICA
Quandoque bonus dormitat Homerus, e figurarsi l'Autore di quest'esercizio!
Non s'è accorto che, per calcolare gli accorciamenti (non allungamenti), bastano due sottrazioni e dare le costanti elastiche è un pleonasmo.
==============================
ALTERNATIVA ORRIBILE
La mia ipotesi ragionevole (estremi fissi, anello mobile) era una bojata pazzesca!

@debbo_rina @Sebastiano
==============================
SECONDA IPOTESI RAGIONEVOLE
* estremi B(- b, - b) e C(c, 0) fissi
* anello ed estremo A(0, 16) mobili
* si devono usare le costanti elastiche (160, 240, 120) N/m
==============================
La situazione di figura è ancora quella deformata, quindi i punti A ed O sono a ordinate superiori a quelle di riposo.
Sull'anello la molla #1 [k*ΔL1 = (160 N/m)*(4/100 m) = 32/5 N] tira in su
* F1(0, 32/5)
ed è equilibrata da
* F2(- 32/5, - 32/5)
* F3(32/5, 0)
---------------
Gli allungamenti risultano
* ΔL = |F|/k
cioè
* ΔL2 = |F2|/k2 = (32/5)*√2/240 = (2/75)*√2 ~= 0.03771236 m
* ΔL3 = |F3|/k3 = (32/5)/120 = 4/75 = 0.05(3) m
valori che sembrano proprio il risultato atteso.
==============================
Il testo è irredimibile: sarebbe bastato un nulla per renderlo umano.

M1 = 160*4 = 640

L1 = 4 cm = 0,04 m 

M2y = M1y = 640

M2x = M2y = 640

M2 = 640√2 

L2 =  640√2 / 240 = (8√2)/3 cm = 3,77 cm = 0,0377 m 

M3 = M2x = 640 

L3 = 640/120 = 16/3 cm = 5,333 cm = 0,05333 m