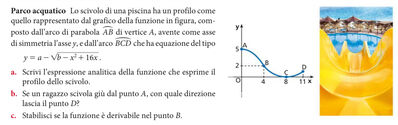
Parco acquatico Lo scivolo di una piscina ha un profilo come quello rappresentato dal grafico della funzione in figura, composto dall'arco di parabola $\overparen{A B}$ di vertice $A$, avente come asse di simmetria l'asse $y$, e dall'arco $\overparen{B C D}$ che ha equazione del tipo $y=a-\sqrt{b-x^2+16 x}$.
a. Scrivi l'espressione analitica della funzione che esprime il profilo dello scivolo.
b. Se un ragazzo scivola giù dal punto $A$, con quale direzione lascia il punto $D$ ?
c. Stabilisci se la funzione è derivabile nel punto $B$.
Buonasera, qualcuno riuscirebbe ad aiutarmi a risolvere questo problema?
Grazie mille