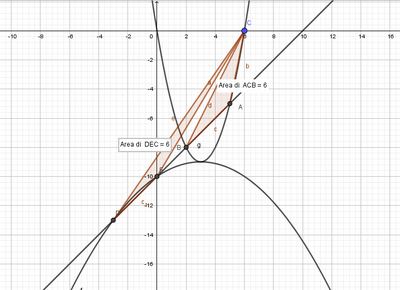
Determina le equazioni delle parabole y = ax^2 + bx + c, aventi per vertice un punto di ordinata - 9 e di ascissa la soluzione minore dell'equazione t^4 - 11 t^3 + 25 t^2 - 11 t + 24 = 0 e che individuano sulla retta x - y - 10 = 0 un segmento AB di misura 3 rad 2. Calcola l'area del triangolo ABC, dove C è l'intersezione di ascissa positiva della parabola, avente la concavità verso l'alto, con l'asse delle x.
Risposte : y = -1/9 x^2 + 2/3 x - 10 ; y = x^2 - 6x ; area = 6
Ho risolto l'equazione che tramite la Regola di Ruffini viene così scomposta : (t-3)(t-8)(t^2 + 1) = 0 le cui radici sono 2, 8 e impossibile. Quindi l'ascissa del vertice dovrebbe essere 3. Poi ho cercato di mettere a sistema l'equazione della parabola con riferimento alle coordinate del vertice con quella della retta, calcolando la distanza fra i punti trovati e ponendola uguale a 3 rad 2, ma non ho abbastanza elementi e quindi mi sono fermato. Grazie come sempre a tutti coloro che vorranno darmi un aiuto.