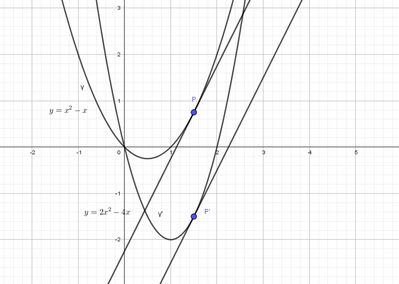
151) Considera le due parabole $\gamma: y=x^2-x$ e $\gamma^{\prime}: y=2 x^2-4 x$. Determina i due punti $P \in \gamma$ e $P^{\prime} \in \gamma^{\prime}$, aventi la stesse ascissa, tali che la tangente a $\gamma$ in $P$ sia parallela alla tangente a $\gamma^{\prime}$ in $P^{\prime}$.
$$
\left[P\left(\frac{3}{2}, \frac{3}{4}\right) ; P^{\prime}\left(\frac{3}{2},-\frac{3}{2}\right)\right.]
$$
potreste svolgerlo, grazie
92
punti
Livello 1
Ciao.
I due punti sulle due parabole hanno stessa ascissa e quindi si possono scrivere come:
[α, α^2 - α]
[α, 2·α^2 - 4·α]
In corrispondenza di tali punti applico le formule di sdoppiamento e mi vado a calcolare le rette tangenti alle due parabole date:
(y + α^2 - α)/2 = α·x - (α + x)/2------> y = x·(2·α - 1) - α^2
(y + 2·α^2 - 4·α)/2 = 2·α·x - 4·(x + α)/2-----> y = 4·x·(α - 1) - 2·α^2
Queste due rette sono parallele se e solo se hanno lo stesso coefficiente angolare:
2·α - 1 = 4·(α - 1)------> α = 3/2
Quindi i due punti P e P':
[3/2, (3/2)^2 - 3/2] = [3/2, 3/4]
[3/2, 2·(3/2)^2 - 4·3/2] = [3/2, - 3/2]
96000
punti
Genius II
@lucianop grazie mille
Due curve distinte hanno tangenti parallele in punti a pari ascissa se è solo se in quell'ascissa hanno eguale pendenza. Nel caso di due parabole le pendenze sono lineari e quindi c'è al più una sola ascissa del genere.
* γ ≡ y = x^2 - x, ha pendenza m(x) = 2*x - 1
* γ' ≡ y = 2*x^2 - 4*x, ha pendenza m'(x) = 4*x - 4
eguagliando le pendenze si ha
* 2*x - 1 = 4*x - 4
da cui
* x = 3/2
* P(3/2, 3/4)
* P'(3/2, - 3/2)
che è proprio il risultato atteso.
57399
punti
Genius I
@exprof scusi ma come ha fatto per ricavare la pendenz
@Francesca1234280
La pendenza del grafico di un polinomio
* y(x) = Σ [k = 0, n] a(k)*x^k
è
* m(x) = Σ [k = 1, n] k*a(k)*x^(k - 1)
