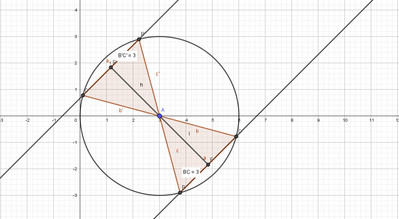
Riscrivo l'equazione della circonferenza applicando la regola del completamento del quadrato:
$x^{2} + y^{2} - 6x + 9 - 9 \,=\, 0 \, \longrightarrow \, (x -3)^{2} + y^{2} \,=\, 9$
La circonferenza ha raggio $3$ ed è centrata in $(3, 0)$
La bisettrice del primo e del terzo quadrante ha formula $y = x$, di conseguenza le rette parallele a questa saranno del tipo $y = x + q$ con $q \in R$.
Ognuna delle rette cercate interseca la circonferenza con una corda lunga $r \,=\, 3$.
Unendo i due estremi di ogni corda con dei segmenti che li collegano al centro della circonferenza si ottiene un triangolo equilatero di lato $3$. La distanza di una corda rispetto al centro della circonferenza vale $\dfrac{\sqrt{3}}{2}3$.
Dalla formula della distanza di un punto da una retta in forma implicita posso ricavarmi i valori di $q$:
$y - x - q \,=\, 0$
$d(P, r) \,=\, \dfrac{|ax_{p} +by_{p} + c|}{\sqrt{a^{2} +b^{2}}}$
$\dfrac{\sqrt{3}}{2}3 \,=\, \dfrac{|-3 + 0 - q|}{\sqrt{2}}\,=\,\dfrac{|-(3 + q)|}{\sqrt{2}}$
$q \,=\, -3 \pm \dfrac{3 \cdot \sqrt{6}}{2}$
L'area del segmento circolare, limitato dal minore dei due archi, si calcola come la differenza tra l'area del settore circolare che insiste sullo stesso arco e e il triangolo che ha come base la corda del segmento circolare.
L'arco di circonferenza ha un ampiezza $\theta$ di $60°$, ha quindi come area $\pi \cdot r^{2} \cdot \dfrac{60°}{360°} \, = \, \dfrac{3}{2}\pi$
L'area del triangolo vale $\dfrac{9\cdot \sqrt{3}}{4}$
L'area del settore circolare vale quindi $\dfrac{3}{2}\pi - \dfrac{9\cdot \sqrt{3}}{4}$