1) Verifica quali tra le seguenti equazioni rappresenta una circonferenza e, in caso affermativo, disegnala
(0.5p ciascuna):
- $3 x^2+3 x+3 y=3 y^2+3$
- $3 x^2+3 x+3 y=-3 y^2-3$
- $3 x^2=-\left(3 y^2-3\right)$
2) Scrivi l'eq. della circonferenza tangente all'asse y di centro $C(-1,-3) .(1.5 p)$
3) Determina la misura della corda che la bisettrice del II e IV quadrante stacca sulla circonferenza di euqzione $x^2+y^2-4 x+7 y=0(1.5 p)$
4) Determina l'equazione della circonferenza avente centro in $C(4 ;-2)$ e tangente alla retta $y=x+2$. $(2 p)$
5) Disegna l'ellisse di equazione $\frac{x^2}{10}+y^2=4$, ricavando la misura dell'eccentricità e le coordinate dei fuochi. (1.5p)
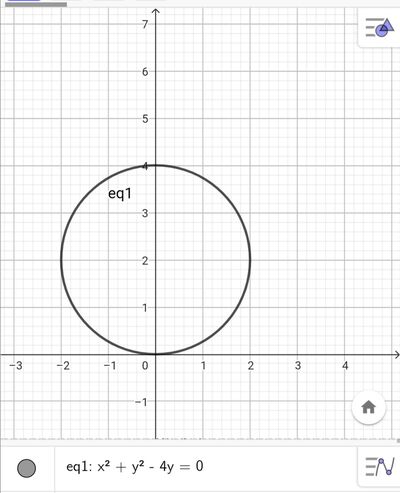
6) Cosa puoi dire sui coefficienti a, b, c dell'equazione di una circonferenza come quella in infigura? (positivi, negativi, nulli..), perché? (1p)
É urgente , Ho bisogno di un’ aiuto per risolvere tutti gli esercizi