II volume del parallelepipedo si calcola moltiplicando l’area di base per la misura dell’altezza. In un parallelepipedo qualsiasi la base è un parallelogramma, e si dice altezza la distanza tra il piano su cui giace la base e il piano su cui giace la faccia ad essa parallela e congruente.
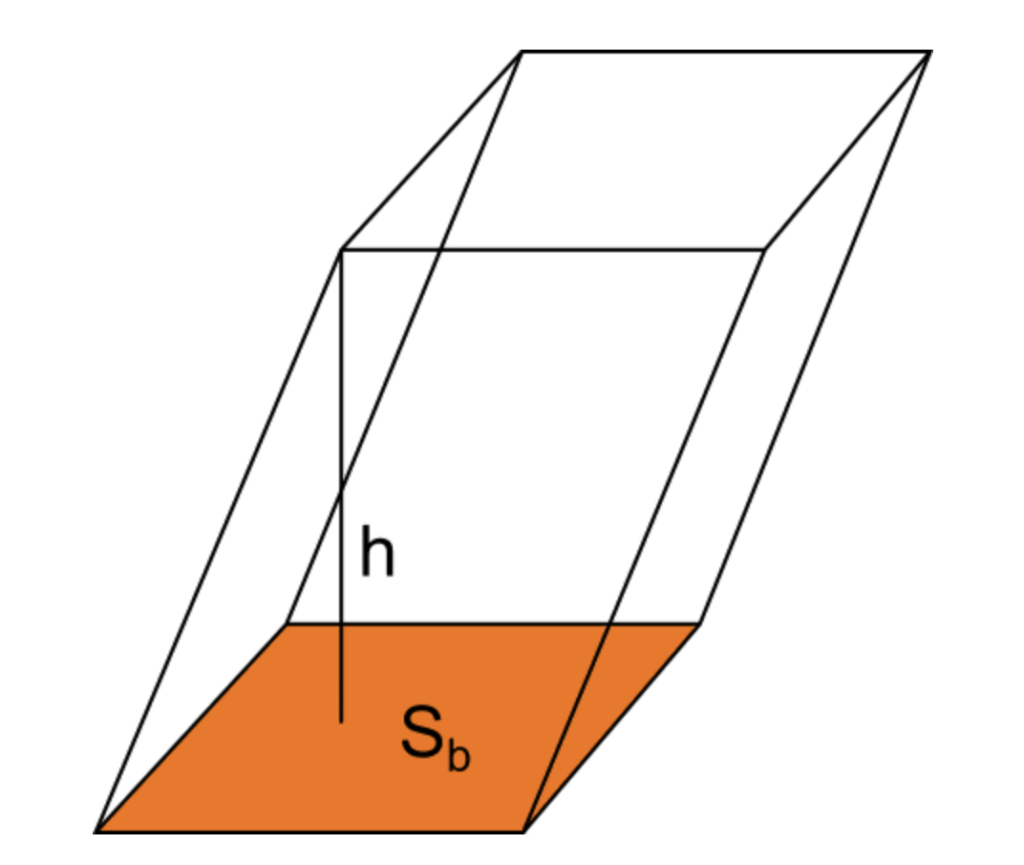
In genere nei problemi di geometria di scuola media e scuola superiore si ha a che fare con il parallelepipedo rettangolo, le cui facce sono sei rettangoli.
Ci occuperemo quindi solo del parallelepipedo rettangolo, la cui altezza coincide con l’altezza di ciascuno dei quattro rettangoli che corrispondono alle facce laterali. Di conseguenza il volume si calcola moltiplicando l’area del rettangolo di base per l’altezza del parallelepipedo.
Formule volume parallelepipedo rettangolo
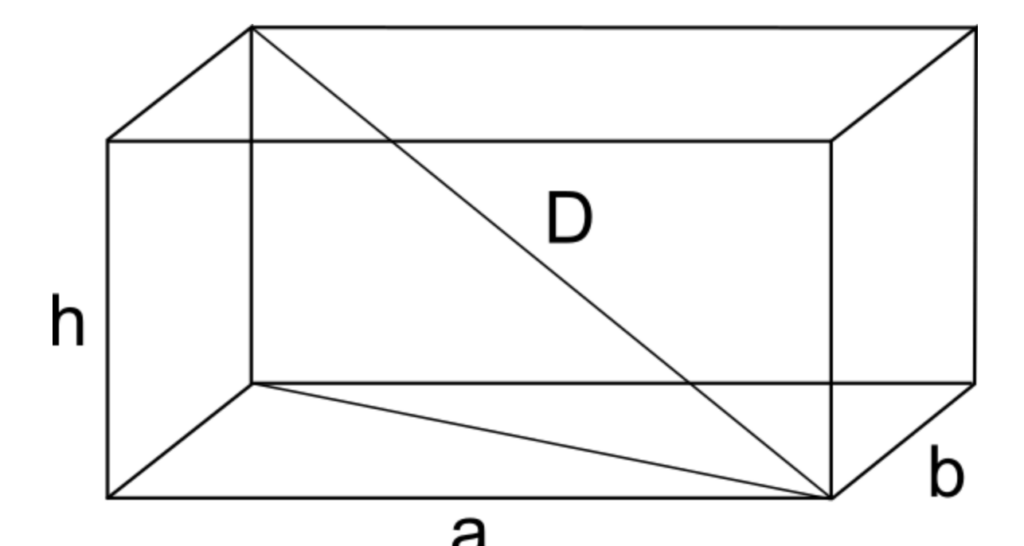
Indichiamo con $a, b$ e $h$ le tre dimensioni del parallelepipedo rettangolo, dove $a$ e $b$ sono le misure di base e altezza del rettangolo di base e $h$ è l’altezza del parallelepipedo. Siano, inoltre, $S_{b}$ l’area della superficie di base e $V$ il volume.
Volume parallelepipedo rettangolo con dimensioni $V=a \cdot b \cdot h$ \
Volume parallelepipedo rettangolo con area di base e altezza & $V=S_{b} \cdot h$ \
Calcolo volume parallelepipedo rettangolo con area di base e altezza
Se sono note l’area del rettangolo di base e la misura dell’altezza, per calcolare il volume si moltipilca l’area di base per l’altezza
$$
V=S_{b} \cdot h
$$
Calcolo volume parallelepipedo rettangolo con le tre dimensioni
Conoscendo le misure delle tre dimensioni del parallelepipedo, dal prodotto tra base e altezza del rettangolo di base si ottiene l’area di base
$$
S_{b}=a \cdot b
$$
dopodiché si può calcolare il volume moltiplicando l’area di base per l’altezza
$$
V=S_{b} \cdot h
$$
In alternativa si può determinare il volume in un solo passaggio, moltiplicando tra loro le misure delle tre dimensioni
$$
V=a \cdot b \cdot h
$$
Calcolo volume parallelepipedo rettangolo con area della superficie totale
Per determinare il volume dall’area della superficie totale si deve necessariamente conoscere la misura di due dimensioni del parallelepipedo. Esse ci permetteranno di risalire alla misura della dimensione incognita, invertendo opportunamente la formula per l’area della superficie totale:
$$
S_{t o t}=2(a b+a h+b h)
$$
Calcolo volume parallelepipedo con area della superficie laterale
L’area della superficie laterale è data dal prodotto tra il perimetro del rettangolo di base e l’altezza del parallelepipedo
$$
S_{\text {lat }}=2 p \cdot h=2(a+b) \cdot h
$$
Per poter determinare il volume dalla superficie laterale il testo del problema deve fornirci qualche altro dato, come la misura di due dimensioni del parallelepipedo o un’altra relazione esistente tra loro.
