Nel caso di un urto anelastico fra due corpi
- la quantità di moto totale si conserva: $\vec{p}{i \text { tot }}=\vec{p}{\text {ftot }}$
- l’energia cinetica totale non si conserva: $K_{\mathrm{i} \mathrm{tot}} \neq K_{\mathrm{f} \text { tot }}$
In particolare, se l’urto è completamente anelastico, i due corpi rimangono «incastrati» dopo l’urto e quindi hanno la stessa velocità finale:
$$\vec{v}_{1 \mathrm{f}}=\vec{v}_{2 \mathrm{f}}=\vec{v}_{\mathrm{f}}$$
Urto anelastico in una direzione
Consideriamo l’urto fra due corpi che si muovono lungo una stessa direzione, come per esempio due carrelli su una rotaia ad aria. Se i carrelli si muovono inizialmente l’uno verso l’altro, urtano in modo anelastico. In genere nell’urto i carrelli non rimangono incastrati, e quindi l’urto non è completamente anelastico. Però durante l’urto si dissipa parte dell’energia iniziale, per esempio sotto forma di suono: il classico rumore dell’urto.
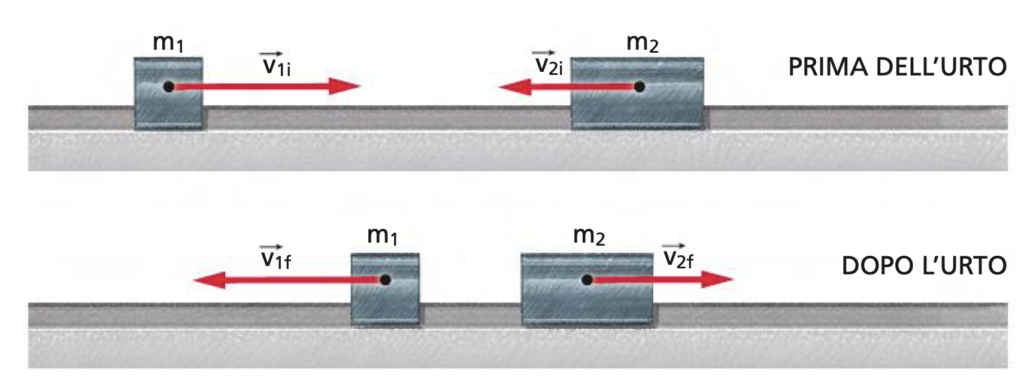
La conservazione della quantità di moto impone che
$$ m_{1} \vec{v}{1 \mathrm{i}}+m_{2} \vec{v}{2 \mathrm{i}}=m_{1} \vec{v}_{1 \mathrm{f}}+m{2} \vec{v}{2 \mathrm{f}} $$
Lungo la direzione del moto, questa equazione si scrive in forma scalare mediante le componenti:
$$ m_{1} v_{1 \mathrm{i}}+m_{2} v_{2 \mathrm{i}}=m_{1} v_{1 \mathrm{f}}+m_{2} v_{2 \mathrm{f}} $$
Nel caso di urto anelastico non esiste un’altra relazione da associare alla precedente, che contiene ben quattro variabili:
$v_{1 \mathrm{i}}, v_{2 \mathrm{i}}, v_{1 \mathrm{f}} \mathrm{e} v_{2 \mathrm{f}}$.
Bisogna quindi conoscere tre di esse per determinare la quarta: per esempio, note le velocità iniziali e la velocità finale di un corpo, si può calcolare la velocità finale dell’altro corpo.
Urto completamente anelastico in una dimensione
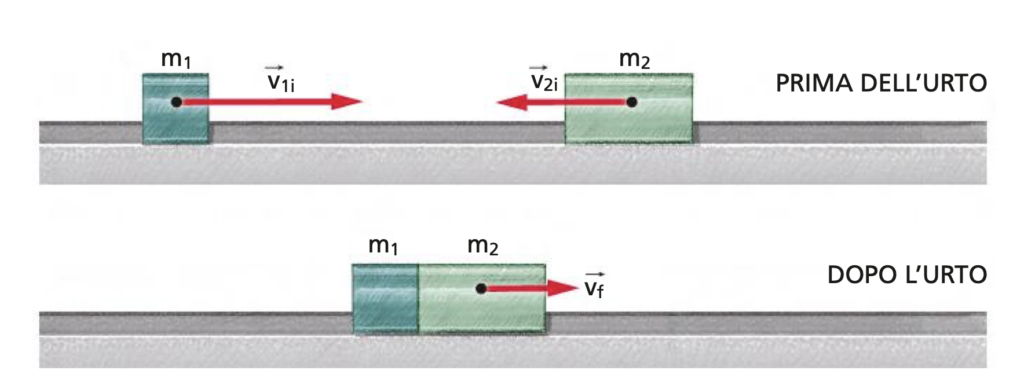
Come nel caso precedente, la conservazione della quantità di moto porta all’equazione scalare
$$
m_{1} v_{1 \mathrm{i}}+m_{2} v_{2 \mathrm{i}}=m_{1} v_{1 \mathrm{f}}+m_{2} v_{2 \mathrm{f}}
$$
Poiché l’urto è completamente anelastico i due corpi hanno la stessa velocità finale $v_{\mathrm{f}}$, per cui risulta:
$$
m_{1} v_{1 \mathrm{f}}+m_{2} v_{2 \mathrm{f}}=\left(m_{1}+m_{2}\right) v_{\mathrm{f}}
$$
Quindi
$$
m_{1} v_{1 \mathrm{i}}+m_{2} v_{2 \mathrm{i}}=\left(m_{1}+m_{2}\right) v_{\mathrm{f}}
$$
Se sono note le velocità iniziali si può calcolare la velocità finale:
$$
v_{\mathrm{f}}=\frac{m_{1} v_{1 \mathrm{i}}+m_{2} v_{2 \mathrm{i}}}{m_{1}+m_{2}}
$$
Supponiamo che il corpo 2 (il bersaglio) sia inizialmente in quiete e venga colpito dal corpo 1 (il proiettile).

La velocità finale del sistema composto dai due corpi incastrati è
$$
v_{\mathrm{f}}=\frac{m_{1}}{m_{1}+m_{2}} v_{1 \mathrm{i}}
$$
Urto completamente anelastico in due dimensioni
Supponiamo che l’urto avvenga su un piano e indichiamo le due direzioni con gli assi $x$ e $y$. La conservazione della quantità di moto
$$
m_{1} \vec{v}_{1 \mathrm{i}}+m_{2} \vec{v}_{2 \mathrm{i}}=m_{1} \vec{v}{1 \mathrm{f}}+m_{2} \vec{v}_{2 \mathrm{f}} $$ è una relazione vettoriale che dà luogo alle due equazioni scalari: $$ \begin{array}{l} m{1} v_{x 1 \mathrm{i}}+m_{2} v_{x 2 \mathrm{i}}=m_{1} v_{x 1 \mathrm{f}}+m_{2} v_{x 2 \mathrm{f}} \
m_{1} v_{y 1 \mathrm{i}}+m_{2} v_{y 2 \mathrm{i}}=m_{1} v_{y 1 \mathrm{f}}+m_{2} v_{y 2 \mathrm{f}}
\end{array}
$$
L’urto è completamente anelastico, quindi i due corpi hanno la stessa velocità finale:
$$
v_{x 1 \mathrm{f}}=v_{x 2 \mathrm{f}}=v_{x \mathrm{f}} \quad v_{y 1 \mathrm{f}}=v_{y 2 \mathrm{f}}=v_{y \mathrm{f}}
$$
Sostituendo nelle equazioni otteniamo in definitiva le due equazioni:
$$m_{1} v_{x 1 \mathrm{i}}+m_{2} v_{x 2 \mathrm{i}}=\left(m_{1}+m_{2}\right) v_{x \mathrm{f}} $$
$$m_{1} v_{y 1 \mathrm{i}}+m_{2} v_{y 2 \mathrm{i}}=\left(m_{1}+m_{2}\right) v_{y \mathrm{f}}$$
