TEOREMA
Due triangoli sono congruenti se hanno ordinatamente congruenti un lato e gli angoli adiacenti al lato.

Utilizzando il metodo di dimostrazione per assurdo, dimostriamo il secondo criterio di congruenza.
In una dimostrazione per assurdo consideriamo vera la negazione della tesi e arriviamo, con una sequenza di deduzioni, a una contraddizione. Questo permette di affermare che la negazione della tesi è falsa e, di conseguenza, la tesi è vera.
DIMOSTRAZIONE
Ragioniamo per assurdo negando la tesi, supponendo cioè che i triangoli non siano congruenti. Deduciamo subito che non può essere $A B \cong A^{\prime} B^{\prime}$, altrimenti i triangoli sarebbero congruenti per il primo criterio. Supponiamo poi che $A B<A^{\prime} B^{\prime}$. Dovrebbe esistere un punto $P$, interno ad $A^{\prime} B^{\prime}$, con $A^{\prime} P \cong A B$
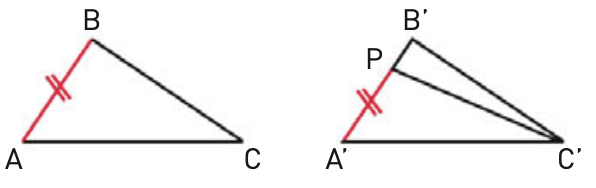
I triangoli $A^{\prime} P C^{\prime}$ e $A B C$ sarebbero congruenti per il primo criterio, avendo $A^{\prime} P \cong A B, A^{\prime} C^{\prime} \cong A C, \widehat{A^{\prime}} \cong \widehat{A}$
In particolare, sarebbe $P \widehat{C^{\prime}} A^{\prime} \cong B \widehat{C} A$. Ma per ipotesi $B \widehat{C} A \cong B^{\prime} \widehat{C^{\prime}} A^{\prime}$, quindi per la proprietà transitiva: $P \widehat{C^{\prime}} A^{\prime} \cong B^{\prime} \widehat{C^{\prime}} A^{\prime}$.
Poiché l’angolo $B^{\prime} \widehat{C^{\prime}} A^{\prime}$ non può essere congruente a una sua parte, siamo giunti a una contraddizione. Allora la negazione della tesi è falsa e i triangoli $A B C$ e $A^{\prime} B^{\prime} C^{\prime}$ sono congruenti. Si procede in modo analogo se si suppone $A B>A^{\prime} B^{\prime}$.
