In questa sezione vengono trattati i numeri primi.
DEFINIZIONE
Un numero, maggiore di 1, divisibile solo per 1 e per se stesso è un numero primo.
I numeri primi sono infiniti: 2,3,5,7,11,13 e li possiamo riassumere nella seguente tabella con un quadrato verde.
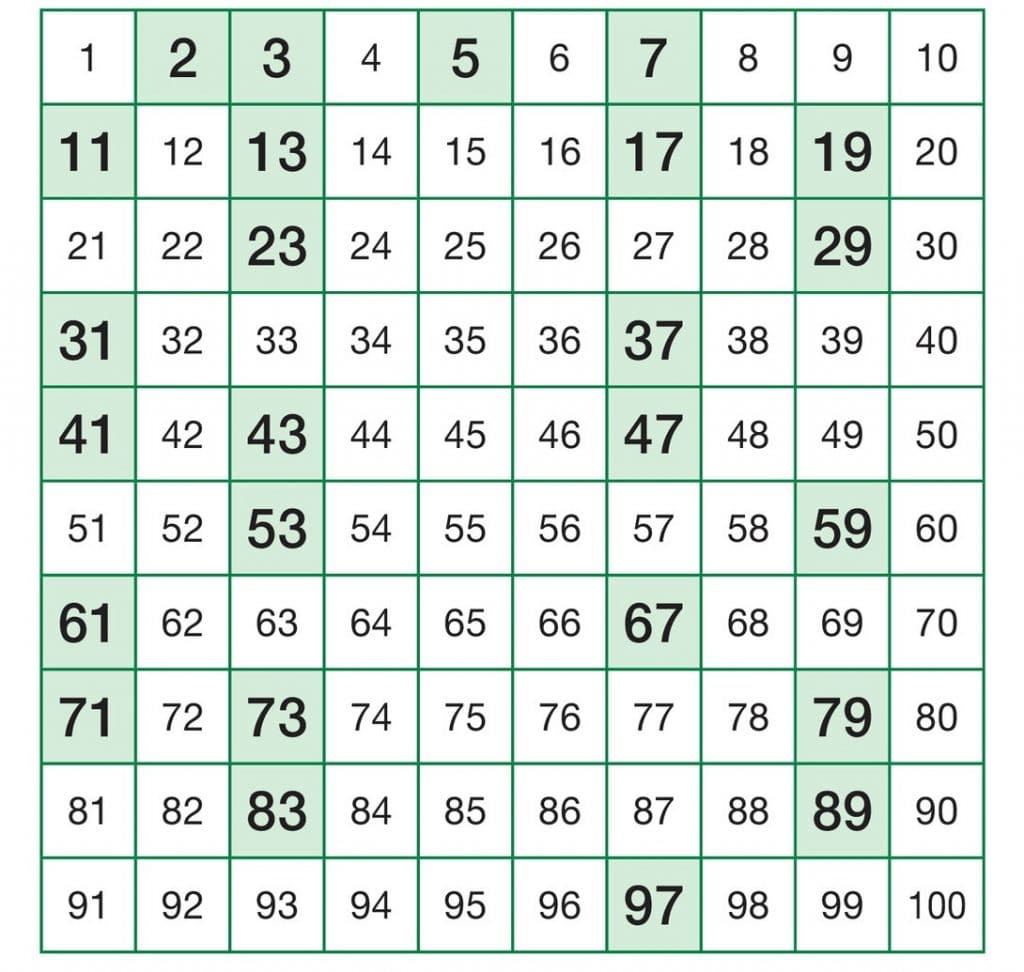
Questa tabella, facilita all’interno di un esercizio, stabilire se un numero è primo o no.
I numeri che hanno più di due divisori, come ad esempio 4,6,8,9,10,12,…, si dicono numeri composti.
OSSERVAZIONE
I numeri pari, ad eccezione del numero 2, non sono primi; quindi possiamo dire che ogni numero primo è dispari.
Non è vero però il viceversa, cioè che tutti i numeri dispari sono primi.
Infatti: 9,15,21,24,27,…, sono dispari, ma non sono primi.
Come stabilire se un generico numero naturale è primo?
A meno che il numero considerato non sia molto grande è semplice stabilire se dato un generico numero naturale maggiore di 1 sia o meno un numero primo. A tale scopo vengono in soccorso i criteri di divisibilità, secondo i quali:
– tutti i numeri che sono pari sono divisibili per 2 e quindi, eccetto 2, non sono primi;
– tutti i numeri che terminano per 5 sono divisibili per 5 e quindi, eccetto 5, non sono primi;
– tutti i numeri la cui somma delle cifre è multiplo di 3 sono divisibili per 3 e quindi, eccetto 3, non sono primi;
– ecc. ecc.
