I teoremi di Euclide riguardano la correlazione tra le lunghezze dei lati di un triangolo rettangolo e le proiezioni dei suoi lati sull’ipotenusa.
– Il primo teorema di Euclide stabilisce che in un triangolo rettangolo ciascun cateto è medio proporzionale tra l’ipotenusa e la proiezione del cateto sull’ipotenusa.
– Il secondo teorema di Euclide stabilisce che in un triangolo rettangolo l’altezza relativa all’ipotenusa è il medio proporzionale tra le proiezioni dei cateti sull’ipotenusa.
Euclide, uno dei pionieri della Geometria Piana nell’Antica Grecia, ha lasciato un’impronta indelebile nel campo matematico. In questa lezione, esamineremo attentamente i due teoremi principali da lui formulati, che riguardano i triangoli rettangoli, e vedremo come possiamo applicare tali concetti nella risoluzione dei problemi.
Proporremo entrambi gli enunciati dei teoremi in due forme equivalenti: una espressa in linguaggio geometrico e l’altra in forma di proporzioni.
Introduzione ai teoremi di Euclide: le proiezioni dei cateti sull’ipotenusa
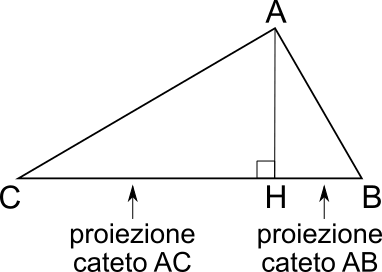
Prima di immergerci nei teoremi di Euclide, è fondamentale acquisire una chiara comprensione del concetto di proiezione di un cateto sull’ipotenusa.
Immaginiamo un triangolo rettangolo $ABC$ con l’angolo retto in $A$. Tracciamo l’altezza relativa all’ipotenusa e identifichiamo con $H$ il punto in cui l’altezza interseca l’ipotenusa.
Il piede dell’altezza suddivide l’ipotenusa in due segmenti, che non sono necessariamente congruenti, indicati rispettivamente come $CH$ e $HB$.
- $CH$ rappresenta la proiezione del cateto $AC$ sull’ipotenusa;
- $BH$ rappresenta la proiezione del cateto $AB$ sull’ipotenusa.
È evidente che la somma delle lunghezze delle proiezioni dei due cateti sull’ipotenusa equivale alla lunghezza dell’ipotenusa stessa:
$$
\overline{C H}+\overline{B H}=\overline{B C}
$$
Primo teorema di Euclide
Il primo teorema di Euclide stabilisce che, all’interno di un triangolo rettangolo, il quadrato costruito su uno dei cateti è equivalente al rettangolo avente come dimensioni l’ipotenusa e la proiezione del cateto sull’ipotenusa.
Questo enunciato mette in connessione tre elementi del triangolo rettangolo: l’ipotenusa, un cateto e la sua proiezione sull’ipotenusa. In particolare, ci riferiamo al primo teorema di Euclide con riferimento al cateto $AB$.
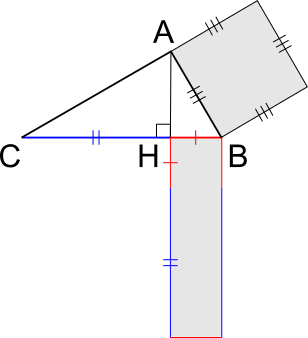
Rispetto alla figura, possiamo ottenere una formula corrispondente al primo teorema di Euclide:
$\overline{AB}^2=\overline{BH} \times \overline{BC}$
Qui, $\overline{AB}^2$ rappresenta l’area del quadrato costruito sul cateto minore, mentre $\overline{BH} \times \overline{BC}$ indica l’area del rettangolo avente come dimensioni la proiezione $BH$ e l’ipotenusa $BC$.
In modo analogo, possiamo formulare la stessa relazione facendo riferimento al cateto maggiore $AC$ e alla sua proiezione $\mathrm{CH}$.
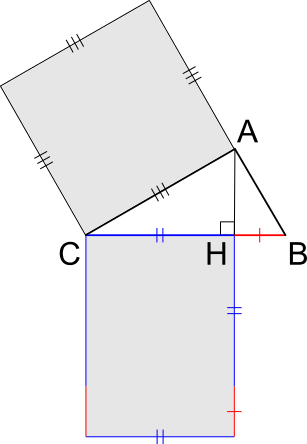
Secondo l’enunciato del primo teorema di Euclide, otteniamo:
$\overline{AC}^2=\overline{CH} \times \overline{BC}$
Ragionando come prima, $\overline{AC}^2$ rappresenta l’area del quadrato costruito sul cateto maggiore, mentre $\overline{CH} \times \overline{BC}$ indica l’area del rettangolo avente come dimensioni la proiezione $CH$ e l’ipotenusa $BC$.
Il primo teorema di Euclide può essere espresso anche attraverso una formulazione equivalente nel linguaggio delle proporzioni: in un triangolo rettangolo, ciascun cateto è medio proporzionale tra l’ipotenusa e la proiezione del cateto sull’ipotenusa.
In termini di proporzioni, ciò si traduce nelle seguenti relazioni:
$\overline{B C}: \overline{A B}=\overline{A B}: \overline{B H} $
$\overline{B C}: \overline{A C}=\overline{A C}: \overline{C H}$
Esempio sul primo teorema di Euclide
Supponiamo di dover calcolare il perimetro di un triangolo rettangolo $ABC$, dove l’angolo retto è in $A$, con ipotenusa di lunghezza $12$ cm e proiezione del cateto minore sull’ipotenusa di lunghezza $5$ cm.
Dati:
$\begin{aligned} & \overline{B C}=12 \mathrm{~cm} \ & \overline{B H}=5 \mathrm{~cm}\end{aligned}$
Utilizzando il primo teorema di Euclide, possiamo calcolare la lunghezza del cateto minore $AB$ tramite la proporzione:
$$
\frac{\overline{B C}}{\overline{A B}}=\frac{\overline{A B}}{\overline{B H}}
$$
Quindi, applicando la proprietà fondamentale delle proporzioni (prodotto dei medi = prodotto degli estremi), otteniamo:
$$
\begin{aligned}
& \overline{A B}^2=\overline{B C} \times \overline{B H} \
& \Rightarrow \overline{A B}=\sqrt{\overline{B C} \times \overline{B H}} \
& =\sqrt{12 \times 5}=\sqrt{60} \approx 7.75 \mathrm{~cm}
\end{aligned}
$$
Quindi, $\overline{AB} \approx 7.75$ cm.
La proiezione relativa al cateto maggiore $AC$ può essere calcolata come differenza tra l’ipotenusa e la proiezione del cateto minore:
$$
\overline{C H}=\overline{B C}-\overline{B H}=(12-5) \mathrm{cm}=7 \mathrm{~cm}
$$
Ora, utilizzando nuovamente il primo teorema di Euclide, possiamo calcolare la lunghezza del cateto maggiore:
$$
\frac{\overline{B C}}{\overline{A C}}=\frac{\overline{A C}}{\overline{C H}}
$$
Applicando la stessa procedura:
$$
\begin{aligned}
& \overline{A C}^2=\overline{B C} \times \overline{C H} \
& \Rightarrow \overline{A C}=\sqrt{B C \times \overline{C H}} \
& =\sqrt{12 \times 7}=\sqrt{84} \approx 9.17 \mathrm{~cm}
\end{aligned}
$$
Quindi, $\overline{AC} \approx 9.17$ cm.
Ora abbiamo tutte le misure necessarie per calcolare il perimetro:
$$
\begin{aligned}
P & =\overline{A B}+\overline{B C}+\overline{A C} \
& =7.75+12+9.17 \
& \approx 29 \mathrm{~cm}
\end{aligned}
$$
Secondo teorema di Euclide
Secondo enunciato di Euclide: in un triangolo rettangolo, il quadrato costruito sull’altezza relativa all’ipotenusa è uguale al rettangolo avente come dimensioni le proiezioni dei cateti sull’ipotenusa. Secondo enunciato di Euclide.
Il secondo teorema di Euclide stabilisce una correlazione tra l’altezza relativa all’ipotenusa e le proiezioni dei cateti su di essa. Facendo riferimento alla figura, possiamo formulare quanto segue:
$$
\overline{A H}^2=\overline{B H} \times \overline{C H}
$$
Analogamente al primo teorema, possiamo esprimere il secondo anche tramite una proporzione: in un triangolo rettangolo, l’altezza relativa all’ipotenusa è il mezzo proporzionale tra le proiezioni dei cateti sull’ipotenusa:
$$
\overline{C H}: \overline{A H}=\overline{A H}: \overline{B H}
$$
Esempio sul secondo teorema di Euclide
Supponiamo di avere un triangolo rettangolo in cui le proiezioni dei cateti sull’ipotenusa sono misurate rispettivamente come $\$ 25 \$ \mathrm{~cm}$ e $\$ 49 \mathrm{~cm}$. Dobbiamo calcolare l’altezza relativa all’ipotenusa.
Dati:
$$
\begin{aligned}
& \overline{B H}=25 \mathrm{~cm} \
& \overline{C H}=49 \mathrm{~cm}
\end{aligned}
$$
Utilizzando la proporzione del secondo teorema di Euclide:
$$
\frac{\overline{C H}}{\overline{A H}}=\frac{\overline{A H}}{\overline{B H}}
$$
Applicando la proprietà fondamentale delle proporzioni (prodotto dei medi $=$ prodotto degli estremi):
$$
\begin{aligned}
& \overline{A H}^2=\overline{C H} \times \overline{B H} \
& \Rightarrow \overline{A H}=\sqrt{\overline{C H} \times \overline{B H}} \
& =\sqrt{49 \times 25}=\sqrt{1225}=35
\end{aligned}
$$
Pertanto, l’altezza misura $35 cm$.
