Per diversi anni i fotoni di Einstein lasciarono nel dubbio il mondo scientifico. Alcuni fisici, tra cui Planck e Lorentz, ritenevano inammissibile che i fotoni fossero una realtà fisica, dato che nei fenomeni di interferenza le radiazioni elettromagnetiche si comportano come onde.
Una decisiva conferma del comportamento corpuscolare delle radiazioni elettromagnetiche giunse però nel 1923 , quando il fisico statunitense Arthur H. Compton (1892- 1962) pubblicò i risultati delle sue ricerche sperimentali sulla diffusione di raggi $\mathrm{X}$ da parte degli elettroni. Le proprietà di questa diffusione, da allora, sono dette effetto Compton.
L’esperimento consisteva nel dirigere un fascio monocromatico di raggi $\mathrm{X}$ contro un bersaglio di grafite e nel misurare la lunghezza d’onda della radiazione diffusa a diversi angoli rispetto alla direzione di incidenza. La lunghezza d’onda dei raggi $\mathrm{X}$ inviati sul bersaglio era $\lambda=0,0709 \mathrm{~nm}=7,09 \times 10^{-11} \mathrm{~m}$
Nello schema sotto, per semplicità, non è rappresentato il monocromatore, cioè il dispositivo che serviva a selezionare la radiazione della lunghezza d’onda voluta; è invece rappresentato il collimatore, il sistema di schermi muniti di fenditura che lasciava passare solo i raggi di una determinata direzione, cioè produceva un fascio parallelo.
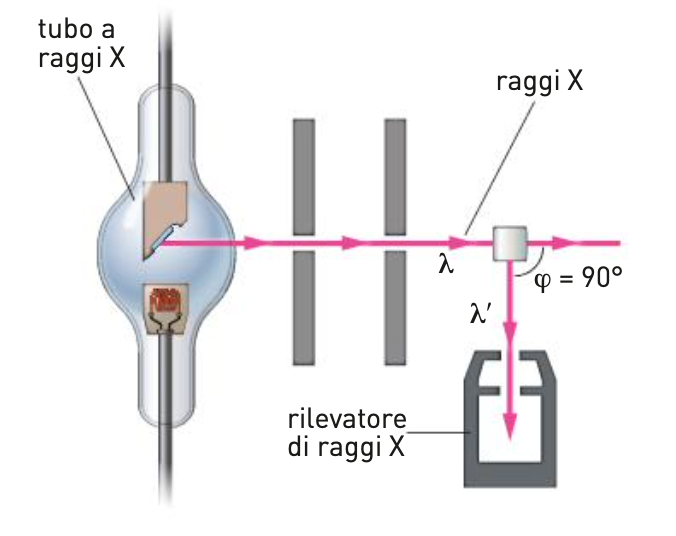
Nell’esperimento di Compton, il fascio monocromatico e parallelo di raggi X colpisce il bersaglio; il rivelatore misura la lunghezza d’onda $\lambda^{\prime}$ della radiazione diffusa a diversi angoli $\varphi$.
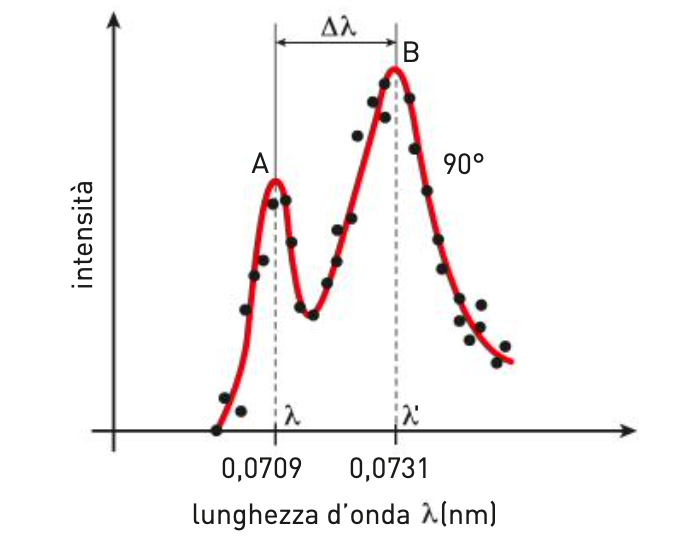
Si trova che, per $\varphi=90^{\circ}$, una parte dei raggi $\mathrm{X}$ diffusi ha la stessa lunghezza d’onda $\lambda$ di quelli incidenti, ma la parte restante ha una lunghezza d’onda media più grande: $\lambda^{\prime}=7,31 \times 10^{-11} \mathrm{~m}$.
L’elettromagnetismo classico non spiega come possa prodursi, nella diffusione delle radiazioni elettromagnetiche, una variazione della lunghezza d’onda.
Secondo la teoria di Maxwell, infatti, gli elettroni che sono investiti da radiazione elettromagnetica di frequenza $f=\frac{c}{\lambda}$ oscillano alla medesima frequenza $f$, per cui emettono una radiazione della stessa lunghezza d’onda $\lambda$ di quella incidente. Le leggi classiche giustificano così il picco $A$ della figura precedente, ma non spiegano il picco $B$.
La lunghezza d’onda del picco $B$, osservato a $90^{\circ}$ dalla direzione di incidenza, è spostata da quella del picco $A$ della quantità
$$
\Delta \lambda=\lambda^{\prime}-\lambda=(7,31-7,09) \times 10^{-11} \mathrm{~m}=0,22 \times 10^{-11} \mathrm{~m}
$$
L’esperienza mostra che $\Delta \lambda$ non dipende dal materiale di cui è fatto il bersaglio, né dalla lunghezza d’onda $\lambda$ della radiazione incidente.
L’interpretazione dell’effetto compton
La presenza e le proprietà del picco B furono spiegate da Compton stesso sulla base dell’ipotesi di Einstein: la radiazione elettromagnetica è composta di fotoni che interagiscono con gli elettroni singolarmente.
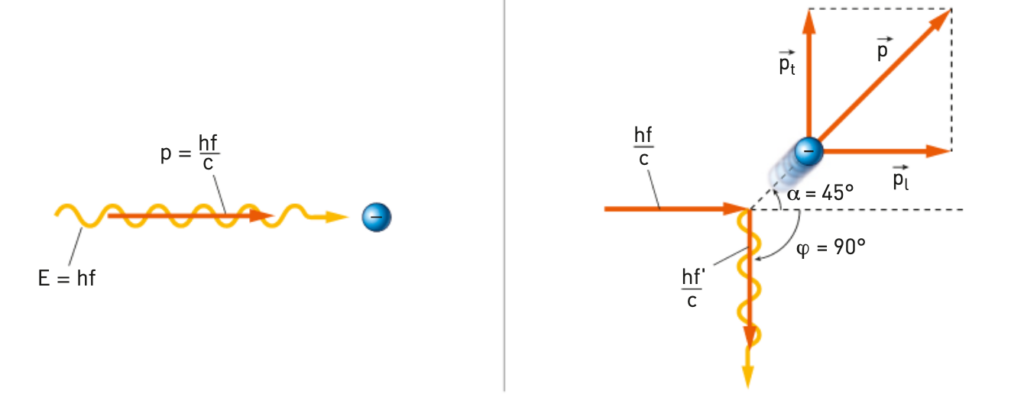
- Linterazione fotone-elettrone è un urto elastico tra particelle. Prima dell’urto, il fotone trasporta un’energia $h f$ e una quantità di moto con modulo $\frac{h f}{c} ;$ l’elettrone, nel bersaglio di grafite, può essere considerato fermo e libero di muoversi.
- Se il fotone è diffuso ad angolo $\varphi=90^{\circ}$, dopo l’urto esso ha energia $h f^{\prime}$ e quantità di moto $\frac{h f^{\prime}}{c} .$ L’elettrone acquista una quantità di moto $\vec{p}$ con componente $p_{l}$ nella direzione di incidenza e componente $p_{t}$ in direzione trasversale.
La quantità di moto dell’elettrone dopo l’urto
Per la conservazione della quantità di moto, le componenti $p_{l} \mathrm{e} p_{t}$ della quantità di moto dell’elettrone hanno, rispettivamente, lo stesso valore della quantità di moto del fotone incidente e della quantità di moto del fotone che emerge dall’urto:
$$
p_{l}=\frac{h f}{c} ; \quad p_{t}=\frac{h f^{\prime}}{c} .
$$
Il risultato sperimentale di Compton mostra che $\lambda$ ‘ differisce di poco da $\lambda$ e quindi $f^{\prime}$ differisce di poco da $f$. Di conseguenza $p_{l}$ e $p_{t}$ sono quasi uguali tra loro.
L’energia cinetica acquistata dall’elettrone
Il fatto che $p_{l}$ sia circa uguale a $p_{t}$ indica che l’elettrone si mette in movimento lungo una direzione inclinata di un angolo $\alpha \cong 45^{\circ}$ rispetto alla direzione del fotone incidente, per cui vale la relazione approssimata $p \cong \sqrt{2} p_{l}$.
Dopo l’urto, l’energia cinetica (non relativistica) dell’elettrone, di massa $m_{e}$ e velocità di modulo $v=\frac{p}{m_{e}}$,
$$
K=\frac{1}{2} m_{e} v^{2}=\frac{p^{2}}{2 m_{e}}=\frac{\left(\sqrt{2} p_{l}\right)^{2}}{2 m_{e}}=\frac{2}{2 m_{e}}\left(\frac{h f}{c}\right)^{2}=\frac{h^{2} f^{2}}{m_{e} c^{2}}
$$
Il risultato di Compton è in accordo con la conservazione dell’energia
Per la conservazione dell’energia, $K$ è uguale alla differenza tra le energie dei due fotoni, cioè si ha $K=h f-h f^{\prime}$, da cui
$$
h f-h f^{\prime}=\frac{h^{2} f^{2}}{m_{e} c^{2}}
$$
Dopo aver diviso i due membri per $h$, si può scrivere questa formula in funzione delle lunghezze d’onda. Si trova
$$
\frac{c}{\lambda}-\frac{c}{\lambda^{\prime}}=\frac{h}{m_{e} \lambda^{2}}
$$
o anche
$$
\frac{c\left(\lambda^{\prime}-\lambda\right)}{\lambda \lambda^{\prime}}=\frac{h}{m_{e} \lambda^{2}}
$$
La trattazione analitica completa dell’urto fotone-elettrone, in cui Compton tenne anche conto della relatività ristretta, fornisce la relazione esatta
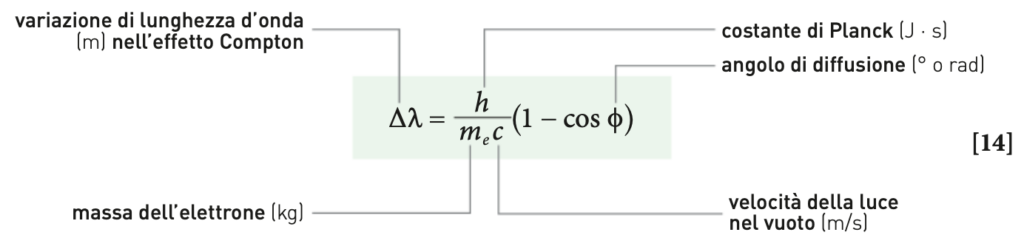
Dopo l’esperimento di Compton, nessuno poteva più avanzare dubbi: i fotoni esistono realmente e possono interagire con la materia in modo individuale, subendo urti elastici descritti dalle stesse leggi che valgono per le particelle.
