Un’equazione o disequazione è irrazionale se in essa ci sono radicali contenenti l’incognita.
Esaminiamo le disequazioni irrazionali del tipo
oppure
, con
intero.
- Se n è dispari, sia la prima sia la seconda disequazione si risolvono elevando alla potenza n-esima entrambi i membri, ottenendo cosi una disequazione equivalente a quella data, cioè:
è equivalente a
;
è equivalente a
.
- Se n è pari, consideriamo il caso n=2 e applichiamo il seguente principio.
Se a e b sono due numeri reali positivi o nulli, la relazione di disuguaglianza che c’è fra i due numeri è la stessa che c’è fra i loro quadrati:
La relazione enunciata nel principio può non essere valida se i due numeri non sono entrambi positivi o nulli.
Nei paragrafi seguenti sono trattate le disequazioni irrazionali applicate ad esercizi svolti.
Le disequazioni del tipo 
La disequazione irrazionale è equivalente al sistema:
ESEMPIO
Risolviamo la disequazione:
Essa è equivalente al sistema:
Ponendo le soluzioni trovate sul grafico, abbiamo:
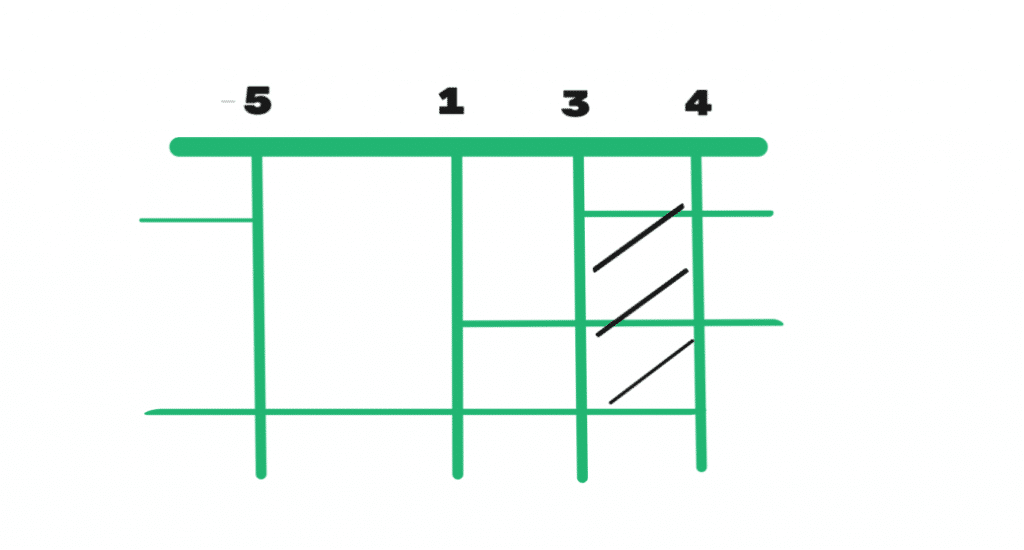
Le soluzioni del sistema, e quindi della disequazione, sono:
Le disequazioni del tipo 
L’insieme delle soluzioni della disequazione irrazionale è l’unione delle soluzioni dei due sistemi:
ESEMPIO
Risolviamo la disequazione:
Otteniamo:
Poniamo i valori trovati sul grafico per vederne la soluzione.
Primo sistema
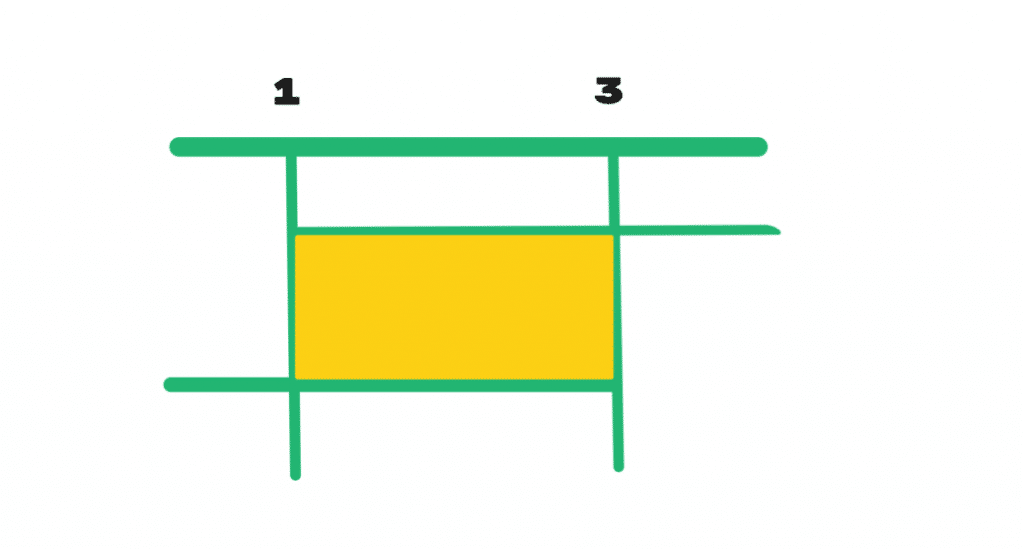
Secondo sistema
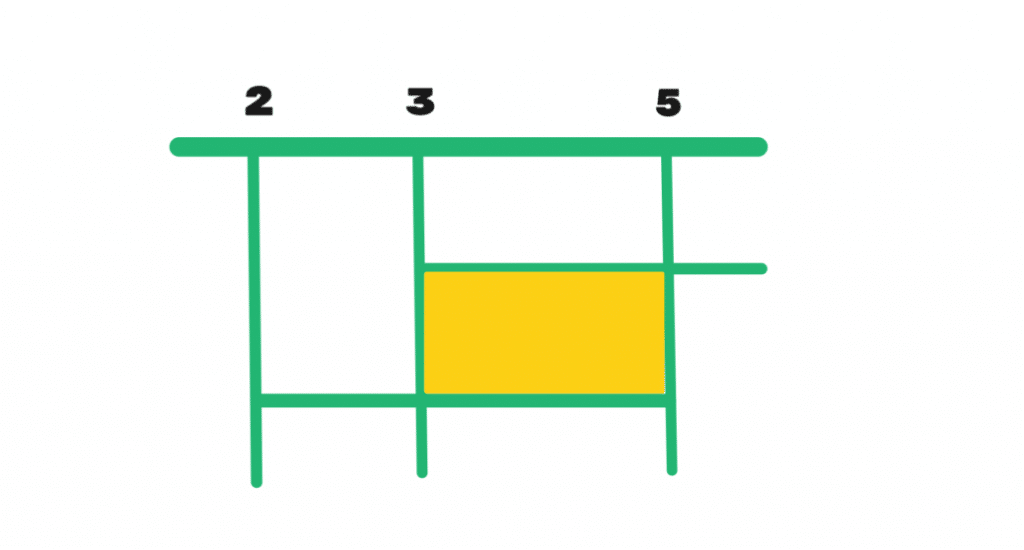
Il primo sistema ha come soluzioni , il secondo
. L’unione dei due intervalli dà l’insieme delle soluzioni della disequazione:
