Il valore assoluto di un numero è uguale al numero stesso se il numero è positivo o nullo, è l’opposto del numero se questo è negativo. In generale:
Vi sono alcune proprietà utili del valore assoluto, riportate qui di seguito.
1) ,
2) ,
3) ,
4) ,
5) ,
6) ,
Di seguito studieremo una disequazione con il valore assoluto, che rappresenta un esercizio tipo.
ESEMPIO
Risolviamo la disequazione con il valore assoluto:
Studiamo il segno all’interno del valore assoluto:
Quindi:
La disequazione ha come soluzioni i valori appartenenti all’unione degli insiemi delle soluzioni dei seguenti sistemi.
Primo sistema

Secondo sistema
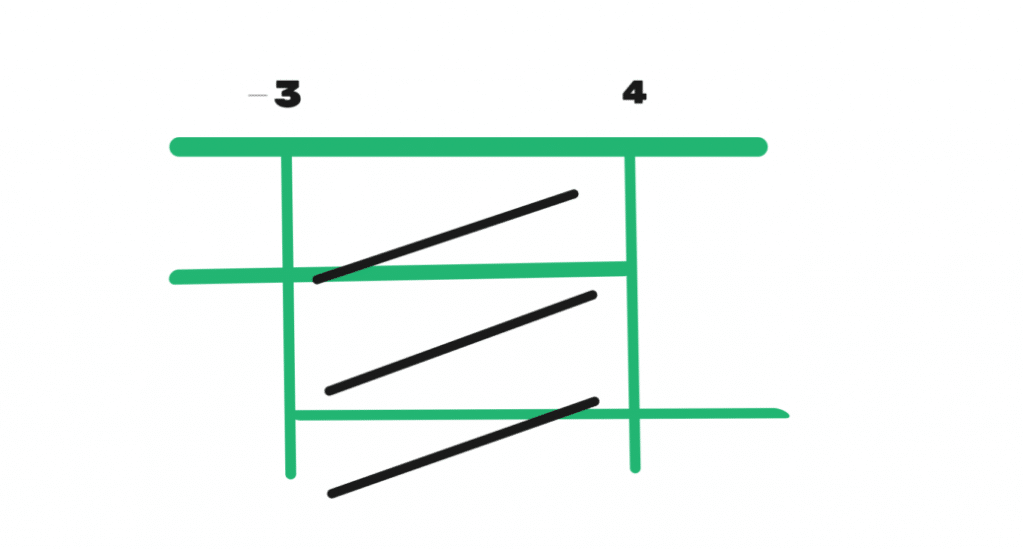
Le soluzioni della disequazione sono quindi:
Particolari disequazioni con il valore assoluto
- Consideriamo le disequazioni con il valore assoluto del tipo |A(x)|< k (con k numero reale positivo).
Se A(x) è una qualsiasi espressione contenente x, si può ricavare che la disequazione:
|A(x)|< k , con k>0,
è equivalente a :
-k < A(x) < k
ossia:
- Consideriamo le disequazioni del tipo |A(x)|> k (con k numero reale positivo).
Se A(x) è una qualsiasi espressione contenente x, si può ricavare che la disequazione:
|A(x)|> k , con k>0,
è equivalente a:
A(x) < -k A(x) > k
ossia l’insieme delle sue soluzioni è l’unione degli insiemi delle soluzioni delle due disequazioni precedenti.
