
Un parcheggiatore ha un tariffario un pò particolare: chiede 1 € per la prima ora di sosta, 0,5 € per la seconda ora di sosta, 0,25 € per la terza ora di sosta, 0,125 € per la quarta ora di sosta e così via. Ipotizzando che un’auto rimanga in sosta per un tempo infinito, se è possibile determinarlo, quanto avrà guadagnato il parcheggiatore? Sarà diventato infinitamente ricco?
SOLUZIONE
[restrict …] Il parcheggiatore vorrà essere corrisposto con un costo che si dimezza continuamente allo scandire delle ore, quindi si ottiene una successione di questo tipo:[restrict]Il parcheggiatore vorrà essere corrisposto con un costo che si dimezza continuamente allo scandire delle ore, quindi si ottiene una successione di questo tipo:
essa rappresenta una serie geometrica:
in cui a è una costante, r è la ragione ed n il termine ennesimo.
In questo caso a = 1 e r = 1/2 .
Le serie geometriche, quando −1 < r < 1 , convergono sempre e quindi forniscono una somma finita anche nel caso di infiniti addendi (come nel caso analizzato), infatti:
perciò, per calcolare il guadagno in un tempo infinito, si imposta la sommatoria:
la quale dimostra che il parcheggiatore è uno sprovveduto, perché anche dopo che è trascorsa una eternità (tempo infinto) avrà guadagnato solamente 2 euro! Rappresentazione grafica della serie geometrica in questione:
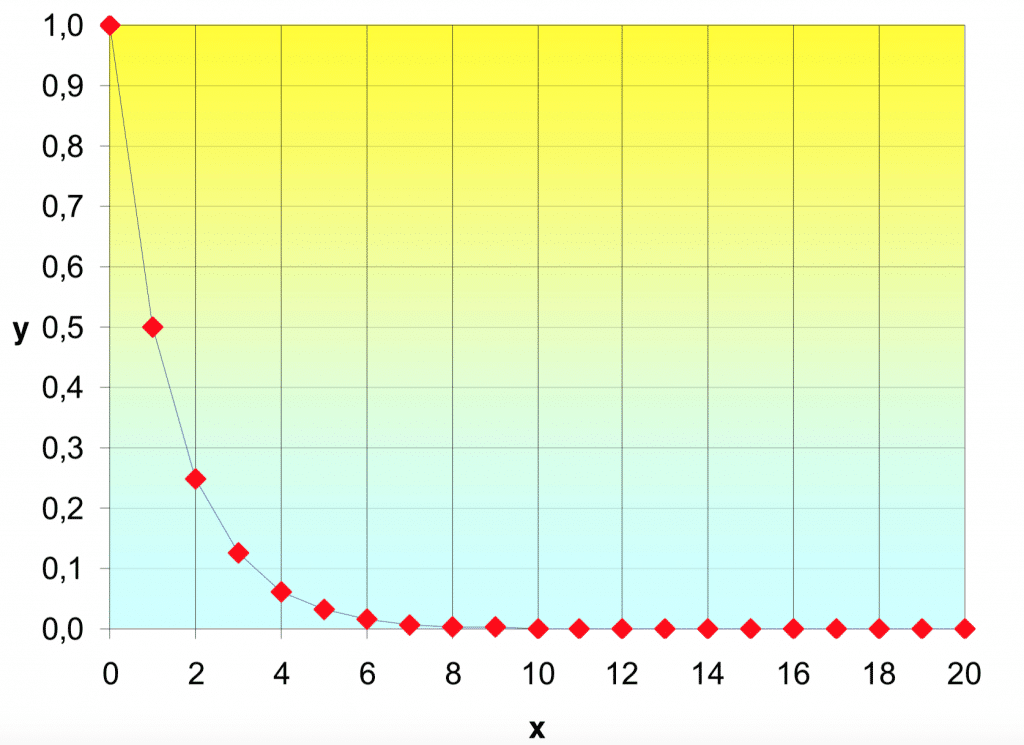
Da notarsi che la serie geometrica è limitata inferiormente dall’asse delle ascisse:
[/restrict]
